
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

【答案】(1)(﹣2,0);(2)①2;②(﹣3,5﹣t);③能确定, z=x+y.
【解析】试题分析:(1)根据平移的性质即可得到结论;
(2)①由点C的坐标为(-3,2).得到BC=3,CD=2,由于点P的横坐标与纵坐标互为相反数;于是确定点P在线段BC上,有PB=CD,即可得到结果;
②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);
③如图,过P作PE∥BC交AB于E,则PE∥AD,根据平行线的性质即可得到结论.
解:(1)根据题意,可得
三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),
∴点E的坐标是(﹣2,0);
故答案为:(﹣2,0);
(2)①∵点C的坐标为(﹣3,2)
∴BC=3,CD=2,
∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,
∴PB=CD,
即t=2;
∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,点P的坐标(﹣t,2),
当点P在线段CD上时,点P的坐标(﹣3,5﹣t);
③能确定,
如图,过P作PF∥BC交AB于F,
则FE∥AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
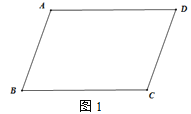
【题目】如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD;
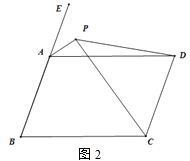
(2)如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.
①求∠APC的度数;
②连接DP,若∠PDC=750,则∠DPC-![]() ∠B=________.
∠B=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把P’(y1,x1)叫做点P的友好点,已知点![]() 的友好点为
的友好点为![]() ,点
,点![]() 的友好点为
的友好点为![]() ,点
,点![]() 的友好点为
的友好点为![]() ,…,这样依次得到点.
,…,这样依次得到点.
(1)当点![]() 的坐标为(2,1),则点
的坐标为(2,1),则点![]() 的坐标为___,点
的坐标为___,点![]() 的坐标为___;
的坐标为___;
(2)若![]() 的坐标为(3,2),则设
的坐标为(3,2),则设![]() (x,y),求x+y的值;
(x,y),求x+y的值;
(3)设点A1的坐标为(a,b),若![]() ,
,![]() ,
,![]() ,…
,…![]() ,点
,点![]() 均在y轴左侧,求a、b的取值范围.
均在y轴左侧,求a、b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
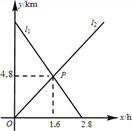
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段![]() 、
、![]() 分别表示小敏、小聪离B地的距离
分别表示小敏、小聪离B地的距离![]() 与已用时间
与已用时间![]() 之间的关系,则小敏、小聪行走的速度分别是
之间的关系,则小敏、小聪行走的速度分别是![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]()
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
(1)如图1可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)比较图1、图2两图的阴影部分面积,可以得到
乘法公式 (用式子表达);
(3)运用你所得到的公式,计算下列各题:
①(2m+n﹣p)(2m﹣n+p) ②10.3×9.7.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制成以下两幅统计图.

根据以上信息,解答下列问题:
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1 800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠BAC=2∠B,∠BAD=∠DAC.说明:∠BAD=∠B.
(2)如图2,已知点E在BA延长线上,∠EAD=∠CAD,∠B=∠C.说明:AD∥BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com