
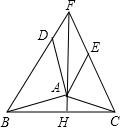
 如图,△ABC中,分别以AB、AC为边向三角形外作△ABD和△ACE,使AD=AB,AE=AC,∠BAD=∠CAE=90°,AH⊥BC,H为垂足,点F在HA的延长线上,且AF=BC,求证:四边形AEFD是平行四边形.
如图,△ABC中,分别以AB、AC为边向三角形外作△ABD和△ACE,使AD=AB,AE=AC,∠BAD=∠CAE=90°,AH⊥BC,H为垂足,点F在HA的延长线上,且AF=BC,求证:四边形AEFD是平行四边形. 分析 首先证明△DAF≌△ABC,推出∠ADF=∠BAC,DF=AC=AE,由∠BAD=∠EAC=90°,推出∠BAC+∠DAE=180°,∠ADF+∠DAE=180°,推出DF∥AE,由此即可证明.
解答 证明: ∵∠BAD=90°,AH⊥BC,
∵∠BAD=90°,AH⊥BC,
∴∠DAF+∠BAH=90°,∠BAH+∠ABC=90°,
∴∠DAF=∠ABC,
在△DAF和△ABC中,
$\left\{\begin{array}{l}{AF=BC}\\{∠DAF=∠ABC}\\{AD=AB}\end{array}\right.$,
∴△DAF≌△ABC,
∴∠ADF=∠BAC,DF=AC=AE,
∵∠BAD=∠EAC=90°,
∴∠BAC+∠DAE=180°,
∴∠ADF+∠DAE=180°,
∴DF∥AE,
∵DF=AE,
∴四边形ADFE是平行四边形.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、平行四边形的判定等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
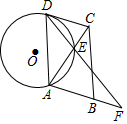 已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.
已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
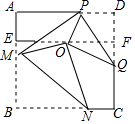 如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.
如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
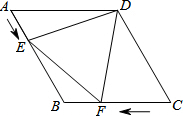 如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )
如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).
在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同旁内角互补,两直线平行 | |
| D. | 互补的两个角一定有一个锐角,一个钝角 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
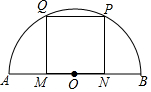 如图,点M,N在半圆的直径AB上,点P,Q在$\widehat{AB}$上,四边形MNPQ为正方形.若半圆的半径为$\sqrt{5}$,则正方形的边长为2.
如图,点M,N在半圆的直径AB上,点P,Q在$\widehat{AB}$上,四边形MNPQ为正方形.若半圆的半径为$\sqrt{5}$,则正方形的边长为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com