
【题目】如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA=_____cm.

科目:初中数学 来源: 题型:
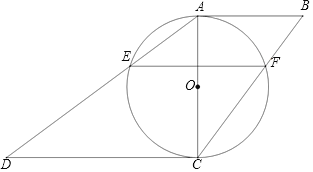
【题目】如图,在四边形ABCD中,AB∥CD,以AC为直径的⊙O交AD于点E,交BC于点F,AB2=BFBC.
(1)求证:AB与⊙O相切;
(2)若![]() .
.
①求证:AC2=ABCD;
②若AC=3,EF=2,则AB+CD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并解答问题:
杨辉和他的一个数学问题

我国古代对代数的研究,特别是对方程的解法研究有着优良的传统并取得了重要成果.
杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述,他著名的数学书共五种二十一卷,它们是:《详解九章算法》12卷(1261年),《日用算法》2卷(1262年),《乘除通变本末》3卷(1274年,第3卷与他人合编),《田(杨辉,南宋数学家)亩比类乘除捷法》2卷(1275年),《续古摘奇算法》2卷(1275年,与他人合编),其中后三种为杨辉后期所著,一般称之为《杨辉算法》.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除捷法》):
直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.
请你用学过的知识解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
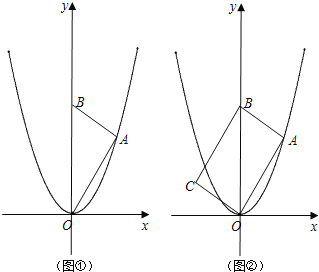
【题目】如图①,在平面直角坐标系中,点A是抛物线y=x2在第一象限上的一个点,连结OA,过点A作AB⊥OA,交y轴于点B,设点A的横坐标为n.
(探究):
(1)当n=1时,点B的纵坐标是 ;
(2)当n=2时,点B的纵坐标是 ;
(3)点B的纵坐标是 (用含n的代数式表示).
(应用):
如图②,将△OAB绕着斜边OB的中点顺时针旋转180°,得到△BCO.
(1)求点C的坐标(用含n的代数式表示);
(2)当点A在抛物线上运动时,点C也随之运动.当1≤n≤5时,线段OC扫过的图形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,AD与BC相交于点E.连接BD,作∠BDF=∠BAD,DF与AB的延长线相交于点F.
(1)求证:DF是⊙O的切线;
(2)若DF∥BC,求证:AD平分∠BAC;
(3)在(2)的条件下,若AB=10,BD=6,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十一”购物街中,某儿童品牌玩具专卖店购进了![]() 两种玩具,其中
两种玩具,其中![]() 类玩具的金价比
类玩具的金价比![]() 玩具的进价每个多
玩具的进价每个多![]() 元.经调查发现:用
元.经调查发现:用![]() 元购进
元购进![]() 类玩具的数量与用
类玩具的数量与用![]() 元购进
元购进![]() 类玩具的数量相同.
类玩具的数量相同.
(1)求![]() 的进价分别是每个多少元?
的进价分别是每个多少元?
(2)该玩具店共购进![]() 了两类玩具共
了两类玩具共![]() 个,若玩具店将每个
个,若玩具店将每个![]() 类玩具定价为
类玩具定价为![]() 元出售,每个
元出售,每个![]() 类玩具定价
类玩具定价![]() 元出售,且全部售出后所获得的利润不少于
元出售,且全部售出后所获得的利润不少于![]() 元,则该淘宝专卖店至少购进
元,则该淘宝专卖店至少购进![]() 类玩具多少个?
类玩具多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
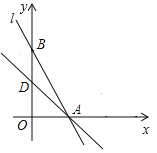
【题目】已知如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于A、B两点(OA<OB),且OA、OB的长分别是一元二次方程x2-18x+72=0的两根,点D为线段OB的中点,过点D作AB的垂线与线段AB相交于点C.
(1)求A、B两点的坐标;
(2)求过点C的反比例函数解析式;
(3)已知点P在直线AD上,在平面内是否存在点Q,使以A、O、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
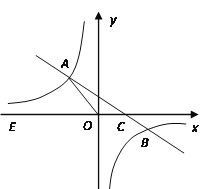
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求△AOB 的面积;
(3)在x轴上是否存在点P,使△APC是直角三角形. 若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com