
【题目】已知![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).连接
重合).连接![]() ,以
,以![]() 为边向逆时针方向作等边
为边向逆时针方向作等边![]() ,连接
,连接![]() ,
,
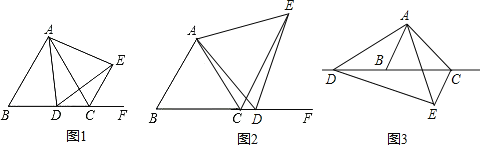
(1)如图1,当点![]() 在边
在边![]() 上时:
上时:
①求证:![]() ;
;
②判断![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)如图2,当点![]() 在边
在边![]() 的延长线上时,其他条件不变,判断
的延长线上时,其他条件不变,判断![]() 之间存在的数量关系,并写出证明过程;
之间存在的数量关系,并写出证明过程;
(3)如图3,当点![]() 在边
在边![]() 的反向延长线上时,其他条件不变,请直接写出
的反向延长线上时,其他条件不变,请直接写出![]() 之间存在的数量关系为 .
之间存在的数量关系为 .
【答案】(1)①见解析;②AC=CE+CD;(2)CE=AC+CD,证明见解析;(3)CD=CE+AC.
【解析】
(1)①根据等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=AC,AD=AE,进而就可以得出△ABD≌△ACE;②由△ABD≌△ACE就可以得出AC=BC=CD+CE;
(2)同(1)先证明△ABD≌△ACE,从而可得出BD=BC+CD=AC+CD=CE;
(3)同(1)先证明△ABD≌△ACE,从而可得出CE+AC=CD.
解:(1)①∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
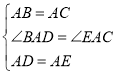 ,
,
∴△ABD≌△ACE(SAS).
②∵△ABD≌△ACE,
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD,
∴AC=CE+CD,
故答案为:AC=CE+CD;
(2)AC+CD=CE.证明如下:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
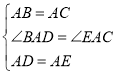 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BD=BC+CD,
∴CE=AC+CD;
(3)DC=CE+BC.证明如下:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠BAD=∠EAC.
在△ABD和△ACE中
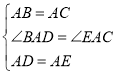 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵CD=BD+BC,
∴CD=CE+AC.
故答案为:CD=CE+AC.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,![]() 与
与![]() 都是等腰直角三角形,直角边
都是等腰直角三角形,直角边![]() ,
,![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 分别是斜边
分别是斜边![]() 、
、![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
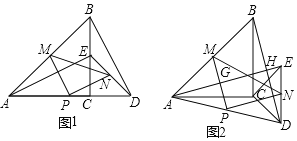
(1)观察猜想:
图1中,![]() 与
与![]() 的数量关系是______,位置关系是______.
的数量关系是______,位置关系是______.
(2)探究证明:
将图1中的![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() (
(![]() ),得到图2,
),得到图2,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,请判断(1)中的结论是否成立,若成立,请证明;若不成立,请说明理由.
,请判断(1)中的结论是否成立,若成立,请证明;若不成立,请说明理由.
(3)拓展延伸:
把![]() 绕点
绕点![]() 任意旋转,若
任意旋转,若![]() ,
,![]() ,请直接列式求出
,请直接列式求出![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由4个全等的正方形组成L形图案,请按下列要求画图:
(1)在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E、 F为AB上的一点,CF⊥AD于H,下列判断正确的有( )

A.AD是△ABE的角平分线B.BE是△ABD边AD上的中线
C.AH为△ABC的角平分线D.CH为△ACD边AD上的高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,
(1)若△ABD的周长是19,AB=7,求BC的长;
(2)求∠BAD的度数.
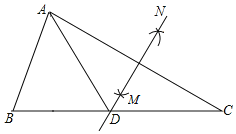
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,反比例函数y=![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式x+b>![]() 的解.
的解.
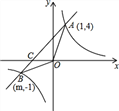
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2米高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13米的距离(点B,F,C在同一条直线上),则AE之间的长为_____米.(结果精确到lm,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)
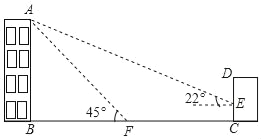
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com