
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
(1)乙车的速度为80km/h(千米/小时);(2)a=40,m=1;(3)甲车共行驶了7h;(4)乙车一定行驶了![]() h或
h或![]() h,两车恰好距离50km.
h,两车恰好距离50km.

A.1个B.2个C.3个D.4个
【答案】B
【解析】
(1)根据函数图象可得乙车行驶3.5-2=1小时与甲车相遇解答;(2)根据乙的速度,求出a的值和m的值解答;(3)再求出甲车行驶的路程y与时间x之间的解析式解答;(4)由解析式之间的关系建立方程解答.
(1)120÷(3.5-2)=80km/h(千米/小时),故正确;
(2)由题意,得
m=1.5-0.5=1.
120÷(3.5-0.5)=40(km/h),
则a=40.故正确
(3)当1.5<x≤7时,甲车y与x之间的函数关系式为y=40x-20,
当y=260时,260=40x-20,
解得:x=7,
∴甲车共行驶时间是7-0.5=6.5小时,故错误
(4)当0≤x≤1时,设甲车y与x之间的函数关系式为y=k1x,由题意,得:
40=k1,
则y=40x
当1<x≤1.5时,
y=40;
当1.5<x≤7时,
设甲车y与x之间的函数关系式为y=k2x+b,由题意,得:
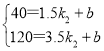 ,
,
解得:k2=40,b=-20,
则y=40x-20.
设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3,由题意得:
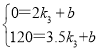 ,
,
解得:k3=80,b=-160,
则y=80x-160.
当40x-20-50=80x-160时,
解得:x=![]() .
.
当40x-20+50=80x-160时,
解得:x=![]() .
.
![]() -2=
-2=![]() ,
,![]() -2=
-2=![]() .
.
所以乙车行驶小时![]() 或
或![]() 小时,两车恰好相距50km,故错误.
小时,两车恰好相距50km,故错误.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)

查看答案和解析>>
科目:初中数学 来源: 题型:
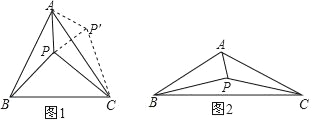
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=![]() ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为 度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为 ;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮参加中华诗词大赛,还剩最后两题,如果都答对,就可顺利通关.其中第一道单选题有4个选项,第二道单选题有3个选项.小亮这两道题都不会,不过还有一个“求助”没有使用(使用求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小亮第一题使用“求助”,那么他答对第一道题的概率是__;
(2)他的亲友团建议:最后一题使用“求助”,从提高通关的可能性的角度看,你同意亲友团的观点吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
(1)求横档AD的长;
(2)点C离地面的高度.(sin15°=0.26,cos15°=0.97,精确到1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com