
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.9 | 9.5 | 9.5 | 8.9 |
| s2 | 0.92 | 0.92 | 1.01 | 1.03 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是-2.
如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
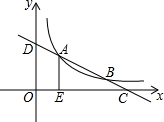 如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.
如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
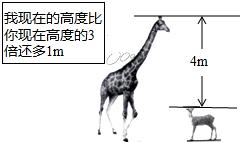 如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.
如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
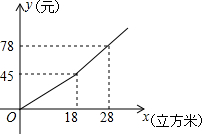 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.| 用水量/立方米 | 水费/元 | |
| 小刚 | 15 | 37.5 |
| 小丽 | 25 | 68.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com