
【题目】如图,在平面直角坐标系中,O 为坐标原点,长方形 OABC,点 B 的坐标为(3,8),点 A、C 分别在坐标轴上,D 为 OC 的中点.
(1)在 x 轴上找一点 P,使得 PD+PB 最小,则点 P 的坐标为 ;
(2)在 x 轴上找一点 Q,使得|QD-QB|最大,求出点 Q 的坐标并说明理由.

【答案】(1) P(1,0);(2)见解析.
【解析】
(1)作点D关于x轴的对称点D',根据轴对称性质有PD=PD',又根据三角形两边之和PD'+PB大于第三边BD',故B、P、D'在同一直线上时,PD+PB有最小值.求直线BD'的解析式后令y=0,求出其与x轴的交点,即此时的点P坐标;
(2)根据三角形两边之差|QD-QB|小于第三边BD,故当B、D、Q在同一直线上时,|QD-QB|=BD有最大值.求直线BD解析式后令y=0,求出此时Q的坐标.
解:(1)作D关于x轴的对称点D',连接BD',交x轴于点P
∵PD=PD'
∴PD+PB=PD'+PB
∴当B、P、D'在同一直线上时,PD+PB=BD'最小
∵四边形OABC是矩形,B(3,8)
∴C(0,8)
∵D为OC中点
∴D(0,4)
∴D'(0,-4)
设直线BD'解析式为:y=kx+b
![]() , 解得:
, 解得:![]() ,
,
∴直线BD':y=4x-4
当4x-4=0时,解得:x=1
故答案为:P(1,0)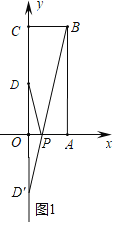
(2)根据三角形两边之差小于第三边,|QD-QB|<BD
∴当B、D、Q在同一直线上时,|QD-QB|=BD最大
设直线BD解析式为:y=ax+c
![]() , 解得:
, 解得:![]()
∴直线BD:y=![]() x+4
x+4
当![]() x+4=0时,解得:x=-3
x+4=0时,解得:x=-3
∴点Q(-3,0)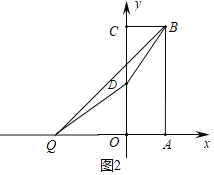


科目:初中数学 来源: 题型:
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41.
≈1.41.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 ![]() 的图象与
的图象与 ![]() 轴交于
轴交于 ![]() (1, 0),
(1, 0), ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,其顶点
,其顶点 ![]() 的坐标为(-3, 2).
的坐标为(-3, 2).
(1)求这二次函数的关系式;
(2)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边AD,CD上,

(1)若AB=6,AE=CF,点E为AD的中点,连接AE,BF.
①如图1,求证:BE=BF=3![]() ;
;
②如图2,连接AC,分别交AE,BF于M,M,连接DM,DN,求四边形BMDN的面积.
(2)如图3,过点D作DH⊥BE,垂足为H,连接CH,若∠DCH=22.5°,则![]() 的值为 (直接写出结果).
的值为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题: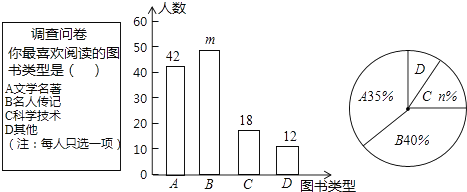
(1)本次调查共抽查了名学生,两幅统计图中的m= , n=.
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com