
【题目】如图,一次函数![]() 的图象与坐标轴交于
的图象与坐标轴交于![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交于
的图象交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,已知
,已知![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点![]() 是
是![]() 轴(除原点
轴(除原点![]() 外)上一点,将线段
外)上一点,将线段![]() 绕点
绕点![]() 按顺时针或逆时针旋转
按顺时针或逆时针旋转![]() 得到线段
得到线段![]() ,当点
,当点![]() 滑动时,点
滑动时,点![]() 能否在反比例函数的图象上?如果能,求出所有的点
能否在反比例函数的图象上?如果能,求出所有的点![]() 的坐标;如果不能,请说明理由.
的坐标;如果不能,请说明理由.
【答案】(1)k2﹣k1=5;(2)![]() ;(3)点Q的坐标为(2+
;(3)点Q的坐标为(2+![]() ,﹣2+
,﹣2+![]() )或(2﹣
)或(2﹣![]() ,﹣2﹣
,﹣2﹣![]() )或(﹣2,﹣2).
)或(﹣2,﹣2).
【解析】
试题分析:(1)根据点M的坐标代入反比例关系![]() 中,可得结论;
中,可得结论;
(2)根据△ACM∽△ADN,得![]() ,由CM=1得DN=4,同理得N的坐标,代入反比例函数式中可得k2的值;
,由CM=1得DN=4,同理得N的坐标,代入反比例函数式中可得k2的值;
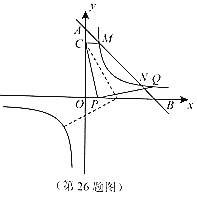
(3)如图2,点P在x轴的正半轴上时,绕P顺时针旋转到点Q,根据△COP≌△PHQ,得CO=PH,OP=QH,设P(x,0),表示Q(x+4,x),代入反比例函数的关系式中可得Q的两个坐标;
如图3,点P在x轴的负半轴上时;
如图4,点P在x轴的正半轴上时,绕P逆时针旋转到点Q,同理可得结论.
试题解析:(1)如图1,∵MC⊥y轴于点C,且CM=1,
∴M的横坐标为1,
当x=1时,y=k1+5,∴M(1,k1+5),
∵M在反比例函数的图象上,∴1×(k1+5)=k2,
∴k2﹣k1=5;
(2)如图1,过N作ND⊥y轴于D,

∴CM∥DN,∴△ACM∽△ADN,∴![]() ,
,
∵CM=1,∴DN=4,
当x=4时,y=4k1+5,∴N(4,4k1+5),∴4(4k1+5)=k2①,
由(1)得:k2﹣k1=5,∴k1=k2﹣5②,
把②代入①得:4(4k2﹣20+5)=k2,k2=4;
∴反比例函数的解析式![]() ;
;
(3)当点P滑动时,点Q能在反比例函数的图象上;
如图2,CP=PQ,∠CPQ=90°,

过Q作QH⊥x轴于H,易得:△COP≌△PHQ,
∴CO=PH,OP=QH,
由(2)知:反比例函数的解析式![]() ;
;
当x=1时,y=4,∴M(1,4),∴OC=PH=4,
设P(x,0),∴Q(x+4,x),
当点Q落在反比例函数的图象上时,x(x+4)=4,x2+4x+4=8,x=﹣2±![]() ,
,
当x=﹣2+![]() 时,x+4=2+
时,x+4=2+![]() ,如图2,Q(2+
,如图2,Q(2+![]() ,﹣2+
,﹣2+![]() );
);
当x=﹣2﹣![]() 时,x+4=2﹣
时,x+4=2﹣![]() ,如图3,Q(2﹣
,如图3,Q(2﹣![]() ,﹣2﹣
,﹣2﹣![]() );
);


如图4,CP=PQ,∠CPQ=90°,设P(x,0),
过P作GH∥y轴,过C作CG⊥GH,过Q作QH⊥GH,
易得:△CPG≌△PQH,∴PG=QH=4,CG=PH=x,∴Q(x﹣4,﹣x),
同理得:﹣x(x﹣4)=4,解得:x1=x2=2,∴Q(﹣2,﹣2),
综上所述,点Q的坐标为(2+![]() ,﹣2+
,﹣2+![]() )或(2﹣
)或(2﹣![]() ,﹣2﹣
,﹣2﹣![]() )或(﹣2,﹣2).
)或(﹣2,﹣2).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB与x轴平行,点A坐标为(3,2),AB=4,则点B的坐标为( )
A.(7,2)B.(-1,2)或(7,2)C.(3,6)D.(3,6)或(3,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.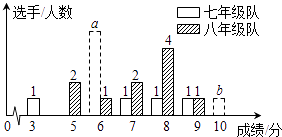
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】频数、频率与实验总次数之间的关系是 ( )
A. 频数越大,频率越大 B. 总次数一定时,频数越大,频率可无限大
C. 频数与总次数成正比 D. 频数一定时,频率与总次数成反比
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com