
分析 (1)将第一个方程代入第二个方程,消去y得到关于x的方程,求出方程的解得到x的值,将x的值代入第一个方程求出y的值,即可得到原方程组的解;
(2)先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解即可.
解答 解:(1)$\left\{\begin{array}{l}{y=2x-3①}\\{4x-3y=1}\end{array}\right.$,
①代入②得:4x-3(2x-3)=1,
整理得:-2x=-8,
解得:x=4,
将x=4代入①得:y=8-3=5,
则原方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+5≤3(x+2)①}\\{\frac{x-1}{2}<\frac{x}{3}②}\end{array}\right.$
由①得x≥-1,
由②得x<3,
所以不等式组的解集是-1≤x<3,
则整数解是-1,0,1,2.
点评 此题考查了解二元一次方程组,利用了消元的思想;也考查不等式(组)的解法;求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.


科目:初中数学 来源: 题型:填空题
 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AM为∠BAC的平分线,若BC=20cm,则AM的长为$\frac{40}{3}$cm.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AM为∠BAC的平分线,若BC=20cm,则AM的长为$\frac{40}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
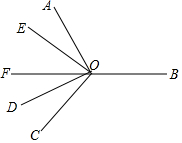 如图,在平面内,∠AOB=∠COB,∠AOD=∠COE=90°,OF平分∠DOE,则以下结论:
如图,在平面内,∠AOB=∠COB,∠AOD=∠COE=90°,OF平分∠DOE,则以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | x>23 | B. | 23<x≤47 | C. | 11≤x<23 | D. | x≤47 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
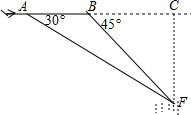 “马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)
“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
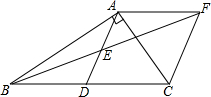 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com