
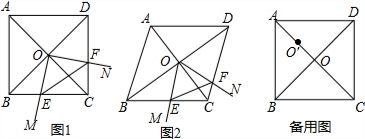
ЗжЮі ЃЈ1ЃЉЁїOEFЪЧЕШбќжБНЧШ§НЧаЮЃЌжЛвЊжЄУїЁїOBEЁеЁїOCFМДПЩЃЎ
ЃЈ2ЃЉЃЉЁїOEFЪЧЕШБпШ§НЧаЮЃЌШчЭМ2ЫљЪОЃКЙ§ЕуOзїOGЁЭBCгыGЃЌзїOHЁЭCDгыHЃЎЯШжЄУїЁїOGEЁеЁїOHFЃЌЕУOE=OFЃЌжЄУїЁЯEOF=60ЁуМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉCE=3$\sqrt{6}$+3$\sqrt{2}$Лђ3$\sqrt{6}$-3$\sqrt{2}$ЃЎМћШчЭМ3жаСНжжЧщаЮЃЌзїOЁфGЁЭBCгкGЃЌOЁфHЁЭCDгкHЃЌжЛвЊжЄУїЁїOGEЁеЁїOHFЭЦГіЁїEOFЪЧЕШбќжБНЧШ§НЧаЮЃЌЧѓГіEGМДПЩНтОіЮЪЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉНсТлЃКЁїOEFЪЧЕШбќжБНЧШ§НЧаЮЃЎ
РэгЩЃКЁпЫФБпаЮABCDЮЊСтаЮЃЌЁЯABC=90ЁуЃЌ
ЁрЫФБпаЮABCDЮЊе§ЗНаЮЃЎ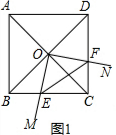
ЁрOB=OCЃЌЁЯOBE=ЁЯOCN=45ЁуЃЌЁЯBOC=90ЁуЃЌЁЯBCD=90ЁуЃЎ
гжЁпЁЯMON+ЁЯBCD=180ЁуЃЌ
ЁрЁЯEOF=90ЁуЃЎ
ЁрЁЯEOC+COF=90ЁуЃЎ
ЁпЁЯBOE+ЁЯEOC=90ЁуЃЌ
ЁрЁЯBOE=ЁЯCOFЃЎ
дкЁїOBEКЭЁїOCFжа
$\left\{\begin{array}{l}{ЁЯOBE=ЁЯOCN=45Ёу}\\{OB=OC}\\{ЁЯBOE=ЁЯCOF}\end{array}\right.$ЃЌ
ЁрЁїOBEЁеЁїOCFЃЌ
ЁрOE=OFЃЎ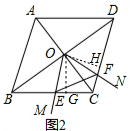
ЁрЁїOEFЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЙЪД№АИЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ2ЃЉНсТлЃКЁїOEFЪЧЕШБпШ§НЧаЮЃЌ
жЄУїЃКШчЭМ2ЫљЪОЃКЙ§ЕуOзїOGЁЭBCгыGЃЌзїOHЁЭCDгыHЃЎ
Й§OзїOGЁЭBCгкGЃЌOHЁЭCDгкHЃЌ
ЁрЁЯOGE=ЁЯOGC=ЁЯOHC=90Ёу
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрCAЦНЗжЁЯBCDЃЌЁЯABC+ЁЯBCD=180ЁуЃЌ
ЁрOG=OHЃЌЁЯBCD=180Ёу-60Ёу=120ЁуЃЌ
ЁпЁЯGOH+ЁЯOGC+ЁЯBCD+ЁЯOHC=360ЁуЃЌ
ЁрЁЯGOH+ЁЯBCD=180ЁуЃЌ
ЁпЁЯMON+ЁЯBCD=180ЁуЃЌ
ЁрЁЯEOF=ЁЯGOH=180Ёу-ЁЯBCD=60ЁуЃЌ
ЁрЁЯEOF-ЁЯGOF=ЁЯGOH-ЁЯGOFЃЌ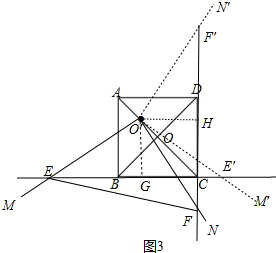
ЁрЁЯEOG=ЁЯFOHЃЌ
дкЁїEOGКЭЁїFOHжаЃЌ
$\left\{\begin{array}{l}{ЁЯEOG=ЁЯFOH}\\{ЁЯOGE=ЁЯOHF}\\{OG=OH}\end{array}\right.$ЃЌ
ЁрЁїOGEЁеЁїOHFЃЌ
ЁрOE=OFЃЌ
ЁпЁЯEOF=60ЁуЃЌ
ЁрЁїEOFЪЧЕШБпШ§НЧаЮЃЎ
ЃЈ3ЃЉCE=3$\sqrt{6}$+3$\sqrt{2}$Лђ3$\sqrt{6}$-3$\sqrt{2}$ЃЎ
РэгЩЃКШчЭМ3жаЃЌЁпСтаЮABCDжаЃЌЁЯABC=90ЁуЃЌ
ЁрЫФБпаЮABCDЪЧе§ЗНаЮЃЌ$\frac{OЁфC}{AC}$=$\frac{3}{4}$ЃЌ
зїOЁфGЁЭBCгкGЃЌOЁфHЁЭCDгкHЃЌ
ЁрЁЯOЁфGC=ЁЯOЁфHC=ЁЯGCH=90ЁуЃЌ
ЁрЫФБпаЮOЁфGCHЪЧОиаЮЃЌ
ЁрOЁфGЁЮABЃЌOЁфHЁЮADЃЌ
Ёр$\frac{OЁфG}{AB}$=$\frac{OЁфH}{AD}$=$\frac{OЁфC}{AC}$=$\frac{3}{4}$ЃЌ
ЁпAB=BC=CD=AD=4$\sqrt{2}$ЃЌ
ЁрOЁфG=OЁфH=3$\sqrt{2}$ЃЌ
ЁрЫФБпаЮOЁфGCHЪЧе§ЗНаЮЃЌ
ЁрCG=OЁфG=3$\sqrt{2}$ЃЌЁЯGOЁфH=90ЁуЃЌ
ЁпЁЯMOЁЯЁфN+ЁЯBCD=180ЁуЃЌЁЯBCD=90ЁуЃЌ
ЁрЁЯEOЁфF=90ЁуЃЌ
ЁрЁЯEOЁфF=ЁЯGOЁфH=90ЁуЃЌ
ЁрЁЯEOЁфG=ЁЯFOЁфHЃЌ
дкЁїEOЁфGКЭЁїFOЁфHжаЃЌ
$\left\{\begin{array}{l}{ЁЯEOЁфG=ЁЯFOЁфH}\\{OЁфG=OЁфH}\\{ЁЯEGOЁф=ЁЯFHOЁф}\end{array}\right.$ЃЌ
ЁрЁїEOЁфGЁеЁїFOЁфHЃЌ
ЁрOЁфE=OЁфFЃЌ
ЁрЁїOЁфEFЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпSЁїABC=$\frac{1}{2}$ЁС4$\sqrt{2}$ЁС4$\sqrt{2}$=16ЃЌ$\frac{{S}_{ЁїABC}}{{S}_{ЁїOEF}}$=$\frac{4}{9}$ЃЌ
ЁрSЁїOEF=36ЃЌ
дкRTЁїOЁфEGжаЃЌEG=$\sqrt{OЁф{E}^{2}-OЁф{G}^{2}}$=3$\sqrt{6}$ЃЌ
ЁрCE=EG+CG=3$\sqrt{6}$+3$\sqrt{2}$ЃЌ
ИљОнЖдГЦадПЩжЊЃЌЕБЁЯMONа§зЊЕНШчЭМЫљЪОЮЛжУЪБЃЌ
CEЁф=EЁфG-CG=3$\sqrt{6}$-3$\sqrt{2}$ЃЎ
злЩЯЫљЪіCE=3$\sqrt{6}$+3$\sqrt{2}$Лђ3$\sqrt{6}$-3$\sqrt{2}$
ЕуЦР БОЬтПМВщЫФБпаЮзлКЯЬтЁЂе§ЗНаЮЕФаджЪЁЂЕШбќжБНЧШ§НЧаЮЕФХаЖЈКЭаджЪЁЂЙДЙЩЖЈРэЁЂШЋЕШШ§НЧаЮЕФХаЖЈКЭаджЪЕШжЊЪЖЃЌНтЬтЕФЙиМќЪЧЬэМгГЃгУИЈжњЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌЪєгкжаПМбЙжсЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ |  | BЃЎ |  | CЃЎ |  | DЃЎ |  |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
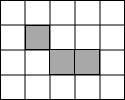 ШчЭМ4ЁС5ЕФЗНИёжНжаЃЌдкГ§вѕгАжЎЭтЕФЗНИёжаШЮвтбЁдёвЛИіЭПКкЃЌгыЭМжавѕгАВПЗжЙЙГЩжсЖдГЦЭМаЮЕФЭПЗЈга4жжЃЎ
ШчЭМ4ЁС5ЕФЗНИёжНжаЃЌдкГ§вѕгАжЎЭтЕФЗНИёжаШЮвтбЁдёвЛИіЭПКкЃЌгыЭМжавѕгАВПЗжЙЙГЩжсЖдГЦЭМаЮЕФЭПЗЈга4жжЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
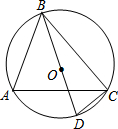 ШчЭМЃЌЁбOЕФжБОЖBD=4ЃЌЁЯA=60ЁуЃЌдђBCЕФГЄЖШЮЊ2$\sqrt{3}$ЃЎ
ШчЭМЃЌЁбOЕФжБОЖBD=4ЃЌЁЯA=60ЁуЃЌдђBCЕФГЄЖШЮЊ2$\sqrt{3}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
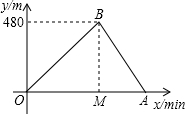 аЁжОКЭаЁУїбЁдёвЛИіЭСЦТНјааХмВНбЕСЗЃЌЫћУЧАДЭЌвЛТЗЯпЭЌЪБГіЗЂЃЌДгЦТНХХмЕНЦТЖЅдйдТЗЗЕЛиЦТНХЃЌСНШЫЩЯЦТЕФЦНОљЫйЖШВЛЭЌЃЌЯТЦТЕФЦНОљЫйЖШдђЪЧИїздЩЯЦТЦНОљЫйЖШЕФ1.5БЖЃЌЩшСНШЫГіЗЂxminКѓОрГіЗЂЕуЕФОрРыЮЊymЃЌЭМжаелЯпБэЪОаЁжОдкећИібЕСЗжаyгыxЕФКЏЪ§ЙиЯЕЃЌЦфжаAЕудкxжсЩЯЃЌMЕузјБъЮЊЃЈ2ЃЌ0ЃЉЃЎ
аЁжОКЭаЁУїбЁдёвЛИіЭСЦТНјааХмВНбЕСЗЃЌЫћУЧАДЭЌвЛТЗЯпЭЌЪБГіЗЂЃЌДгЦТНХХмЕНЦТЖЅдйдТЗЗЕЛиЦТНХЃЌСНШЫЩЯЦТЕФЦНОљЫйЖШВЛЭЌЃЌЯТЦТЕФЦНОљЫйЖШдђЪЧИїздЩЯЦТЦНОљЫйЖШЕФ1.5БЖЃЌЩшСНШЫГіЗЂxminКѓОрГіЗЂЕуЕФОрРыЮЊymЃЌЭМжаелЯпБэЪОаЁжОдкећИібЕСЗжаyгыxЕФКЏЪ§ЙиЯЕЃЌЦфжаAЕудкxжсЩЯЃЌMЕузјБъЮЊЃЈ2ЃЌ0ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com