
【题目】如图,AB∥DE,∠1=∠ACB,AC平分∠BAD,
(1)试说明: AD∥BC.
(2)若∠B=80°,求∠ADE的度数.
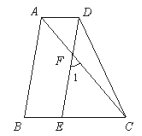
【答案】(1)证明见解析;(2)∠ADE=80°
【解析】
(1)根据平行线的性质与判定,两直线平行,即∠1=∠BAC,再利用角平分线的性质,得出∠1=∠DAC,进而得出∠DAC=∠ACB,即可得证;
(2)根据AB∥DE,AD∥BC,得出∠B=∠ADE,进而求出∠ADE的度数.
(1)证明:∵AB∥DE(已知),
∴∠1=∠BAC(两直线平行,同位角相等),
∵AC平分∠BAD(已知),
∴∠BAC=∠DAC,
∴∠1=∠DAC(等量代换),
∵∠1=∠ACB(已知),
∴∠DAC=∠ACB(等量代换),
∴AD∥BC(内错角相等,两直线平行).
(2)证明:∵AB∥DE,AD∥BC,
∴∠B=∠DEC,∠DEC=∠ADE,
∴∠B=∠ADE,
∵∠B=80°,
∴∠ADE=80°.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)2xy-![]() (4xy-8x2y2)+2(3xy-5x2y2),其中x=
(4xy-8x2y2)+2(3xy-5x2y2),其中x=![]() ,y=-3.
,y=-3.
(2)-a2b+(3ab2-a2b)-2(2ab2-a2b),其中a=1,b=-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,CA平分∠DCB,∠ADC=∠BAC=90°. 
(1)求证:AC2=BCDC;
(2)若BC=5,DC=1,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
A.始终不变
B.先减小后增大
C.一直变大
D.一直变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中,装有10个红球、2个黄球、8个篮球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个红球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率是 ![]() ,问取出了多少个红球?
,问取出了多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(0,8),(﹣3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=﹣2x2+bx+c经过点(0,4),(﹣1,﹣2),设运动时间为t秒.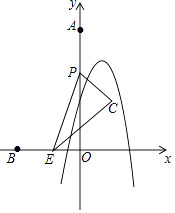
(1)求该抛物线的表达式;
(2)当t=2时,求点C的坐标;
(3)①当t<3时,求点C的坐标(用含t的代数式表示);
②在运动过程中,若点C恰好落在该抛物线上,请直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
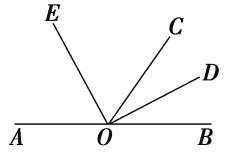
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com