
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
| x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
分析 (1)由表中数据可直接得出;
(2)建立坐标系后,根据顶点坐标(1,0.45),设解析式为y=m(x-1)2+0.45,将(0,0.25)代入即可求得其解析式,再令y=0求得x即可;
(3)①将(2)中所得点的坐标(2.5,0)代入即可;
②由球网高度及球桌的长度可知其扣杀路线解析式为y=$\frac{1}{10}$x,若要击杀则有a(x-3)2-$\frac{1}{4}$a=$\frac{1}{10}$x,根据有唯一的击球点即该方程有唯一实数根即可求得a的值,继而根据对应x的值取舍可得.
解答 解:(1)由表格中数据可知,当t=0.4秒时,乒乓球达到最大高度.
(2)以点A为原点,桌面中线为x轴,乒乓球水平运动方向为正方向建立直角坐标系.
由表格中数据可判断,y是x的二次函数,且顶点为(1,0.45),
所以可设y=m(x-1)2+0.45,
将(0,0.25)代入,得:0.25=m(0-1)2+0.45,
解得:m=-0.2,
∴y=-0.2(x-1)2+0.45.
当y=0时,-0.2(x-1)2+0.45=0,
解得:x=2.5或x=-0.5(舍去).
∴乒乓球落在桌面时,与端点A的水平距离是2.5米.
(3)①由(2)得,乒乓球落在桌面时的坐标为(2.5,0).
∴将(2.5,0)代入y=a(x-3)2+k,得0=a(2.5-3)2+k,
化简整理,得:k=-$\frac{1}{4}$a.
②由题意可知,扣杀路线在直线y=$\frac{1}{10}$x上,
由①得y=a(x-3)2-$\frac{1}{4}$a,
令a(x-3)2-$\frac{1}{4}$a=$\frac{1}{10}$x,整理,得20ax2-(120a+2)x+175a=0.
当△=(120a+2)2-4×20a×175a=0时,符合题意,
解方程,得a1=$\frac{-6+\sqrt{35}}{10}$,a2=$\frac{-6-\sqrt{35}}{10}$.
当a=$\frac{-6+\sqrt{35}}{10}$时,求得x=-$\frac{\sqrt{35}}{2}$,不合题意,舍去;
当a=$\frac{-6-\sqrt{35}}{10}$时,求得x=$\frac{\sqrt{35}}{2}$,符合题意.
答:当a=$\frac{-6-\sqrt{35}}{10}$时,可以将球沿直线扣杀到点A.
点评 本题主要考查二次函数的实际应用,由实际问题建立起二次函数的模型并将二次函数的问题转化为一元二次方程求解是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
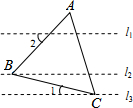 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 为抵御百年不遇的洪水,某市政府决定将1200m长的大堤的迎水坡面铺石加固,堤高DF=4m,堤面加宽2m,则完成这一工程需要的石方数为144000m3.
为抵御百年不遇的洪水,某市政府决定将1200m长的大堤的迎水坡面铺石加固,堤高DF=4m,堤面加宽2m,则完成这一工程需要的石方数为144000m3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com