
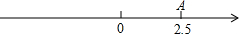 探索性问题:
探索性问题:


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏灌南实验中学七年级第一次阶段性检测数学试卷(带解析) 题型:解答题
探索性问题:
如图,已知A,B在数轴上分别表示a、b。利用数形结合思想回答下列问题:
(1)填写下表:
(2)任取上表一列数,你发现距离表示列式为 (用a、b表示),
则轴上表示 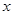 和
和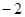 的两点之间的距离表示为 .
的两点之间的距离表示为 .
(3)若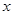 表示一个有理数,且
表示一个有理数,且 ,则
,则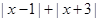 = .
= .
(4)若A,B两点的距离为 d,则d与a、b有何数量关系。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏灌南实验中学七年级第一次阶段性检测数学试卷(解析版) 题型:解答题
探索性问题:
如图,已知A,B在数轴上分别表示a、b。利用数形结合思想回答下列问题: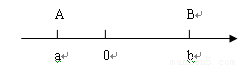
(1)填写下表:

(2)任取上表一列数,你发现距离表示列式为 (用a、b表示),
则轴上表示  和
和 的两点之间的距离表示为
.
的两点之间的距离表示为
.
(3)若 表示一个有理数,且
表示一个有理数,且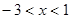 ,则
,则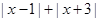 =
.
=
.
(4)若A,B两点的距离为 d,则d与a、b有何数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com