

 ×2x(5-x),令该式等于4,列出方程求出符合题意的解;
×2x(5-x),令该式等于4,列出方程求出符合题意的解; ×2x(5-x)=7,化简该方程后,判断该方程的△与0的关系,大于或等于0则可以,否则不可以.
×2x(5-x)=7,化简该方程后,判断该方程的△与0的关系,大于或等于0则可以,否则不可以. BP•BQ=4,得
BP•BQ=4,得 (5-x)2x=4.
(5-x)2x=4. (5-x)2x=7.
(5-x)2x=7.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
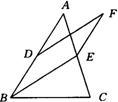 19、如图所示,已知在△ABC中,D是AB的中点,E是AC上的点,且∠ABE=∠BAC,EF∥AB,DF∥BE,请猜想DF与AE有怎样的关系,并说明理由.
19、如图所示,已知在△ABC中,D是AB的中点,E是AC上的点,且∠ABE=∠BAC,EF∥AB,DF∥BE,请猜想DF与AE有怎样的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
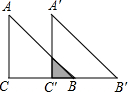 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com