
ЁОЬтФПЁПаЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
![]() здБфСПxЕФШЁжЕЗЖЮЇЪЧШЋЬхЪЕЪ§ЃЌxгыyЕФМИзщЖдгІЪ§жЕШчЯТБэЃК
здБфСПxЕФШЁжЕЗЖЮЇЪЧШЋЬхЪЕЪ§ЃЌxгыyЕФМИзщЖдгІЪ§жЕШчЯТБэЃК
x |
|
|
|
|
|
|
|
|
| 0 |
|
| 1 |
|
| 2 |
|
|
|
y |
|
|
| 0 |
|
| 0 |
|
| 4 |
|
| 0 |
|
| m |
|
|
|
Цфжа![]() _______ЃЛ
_______ЃЛ
![]() ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌАбИУКЏЪ§ЕФЭМЯѓВЙГфЭъећЃЛ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌАбИУКЏЪ§ЕФЭМЯѓВЙГфЭъећЃЛ
![]() ЙлВьКЏЪ§ЭМЯѓЃЌаДГівЛЬѕИУКЏЪ§ЕФаджЪ______ЃЛ
ЙлВьКЏЪ§ЭМЯѓЃЌаДГівЛЬѕИУКЏЪ§ЕФаджЪ______ЃЛ
![]() НјвЛВНЬНОПКЏЪ§ЭМЯѓЗЂЯжЃК
НјвЛВНЬНОПКЏЪ§ЭМЯѓЗЂЯжЃК
![]() ЗНГЬ
ЗНГЬ![]() га______ИіЛЅВЛЯрЕШЕФЪЕЪ§ИљЃЛ
га______ИіЛЅВЛЯрЕШЕФЪЕЪ§ИљЃЛ
![]() гаСНИіЕу
гаСНИіЕу![]() КЭ
КЭ![]() дкДЫКЏЪ§ЭМЯѓЩЯЃЌЕБ
дкДЫКЏЪ§ЭМЯѓЩЯЃЌЕБ![]() ЪБЃЌБШНЯ
ЪБЃЌБШНЯ![]() КЭ
КЭ![]() ЕФДѓаЁЙиЯЕЮЊЃК
ЕФДѓаЁЙиЯЕЮЊЃК![]() ______
______![]() ЬюЁА
ЬюЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБ
ЁБ![]() ЃЛ
ЃЛ
![]() ШєЙигкxЕФЗНГЬ
ШєЙигкxЕФЗНГЬ![]() га4ИіЛЅВЛЯрЕШЕФЪЕЪ§ИљЃЌдђaЕФШЁжЕЗЖЮЇЪЧ______ЃЎ
га4ИіЛЅВЛЯрЕШЕФЪЕЪ§ИљЃЌдђaЕФШЁжЕЗЖЮЇЪЧ______ЃЎ
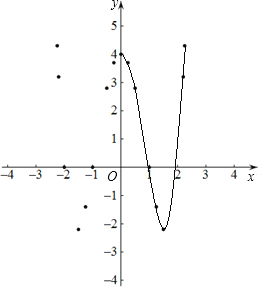
ЁОД№АИЁПЃЈ1ЃЉ0ЃЛЃЈ2ЃЉЭМЯёМћЯъНтЃЛЃЈ3ЃЉКЏЪ§ЭМЯѓЙигкyжсЖдГЦЃЛЃЈ4ЃЉЂй4ЃЛЂкЃМЃЛЂл-2.2ЃМaЃМ4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙлВьЖдгІЪ§жЕБэМДПЩЕУГіЃЛ
ЃЈ2ЃЉгУЦНЛЌЕФЧњЯпвРДЮСЌНгЭМжаЫљУшЕФЕуМДПЩЃЛ
ЃЈ3ЃЉЙлВьКЏЪ§ЭМЯѓЃЌМДПЩЧѓЕУЃЎ
ЃЈ4ЃЉЂйгЩКЏЪ§ЭМЯёгыxжсЕФНЛЕуЃЌМДПЩЕУЕНД№АИЃЛ
ЂкгЩЭМЯёПЩжЊЃЌ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌМДПЩЕУЕНД№АИЃЛ
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌМДПЩЕУЕНД№АИЃЛ
ЂлевГіКЏЪ§ЕФзюДѓжЕКЭзюаЁжЕЃЌНсКЯЭМЯёЃЌМДПЩЕУЕНД№АИ.
НтЃКЃЈ1ЃЉЙлВьЖдгІЪ§жЕБэПЩжЊЃКm=0ЃЌ
ЙЪД№АИЮЊЃК0ЃЛ
ЃЈ2ЃЉгУЦНЛЌЕФЧњЯпвРДЮСЌНгЭМжаЫљУшЕФЕуЃЌШчЯТЭМЫљЪОЃК
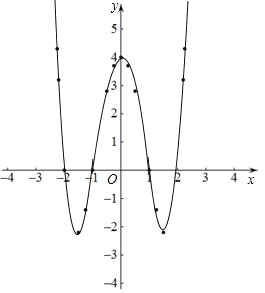
ЃЈ3ЃЉЙлВьКЏЪ§ЭМЯѓЃЌЗЂЯжИУКЏЪ§ЭМЯѓЙигкyжсЖдГЦЃЌЃЈД№АИВЛЮЈвЛЃЉЃЌ
ЙЪД№АИЮЊЃККЏЪ§ЭМЯѓЙигкyжсЖдГЦЃЛ
ЃЈ4ЃЉЂйЁпКЏЪ§ЕФЭМЯѓгыxжсга4ИіНЛЕуЃЌ
ЁрЗНГЬx4-5x2+4=0га4ЛЅВЛЯрЕШЕФЪЕЪ§ИљЃЌ
ЙЪД№АИЮЊЃК4ЃЛ
ЂкКЏЪ§ЭМЯѓПЩжЊЃЌЕБx2ЃОx1ЃО2ЪБЃЌy1ЃМy2ЃЛ
ЙЪД№АИЮЊЃКЃМЃЛ
ЂлЙлВьКЏЪ§ЭМЯѓЃЌ
КЏЪ§ЕФзюДѓжЕЮЊЃК4ЃЌзюаЁжЕЮЊЃК-2.2ЃЛ
НсКЯЖдгІЪ§жЕБэПЩжЊЃК-2.2ЃМaЃМ4ЃЌ
ЙЪД№АИЮЊЃК-2.2ЃМaЃМ4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДКМОе§ЪЧаТЯЪВннЎЩЯЪаЕФМОНкЃЌМзЁЂввСНМвЫЎЙћЕъЃЌЦНЪБвдЭЌбљЕФМлИёГіЪлЦЗжЪЯрЭЌЕФВннЎЃЌЁАВннЎНкЁБЦкМфЃЌМзЁЂввСНМвЩЬЕъЖМШУРћГъБіЃЌЙЫПЭЕФелКѓИЖПюН№Жю![]() ЁЂ
ЁЂ![]() ЃЈЕЅЮЛЃКдЊЃЉгыБъМлгІИЖПюН№ЖюxЃЈЕЅЮЛЃКдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈЕЅЮЛЃКдЊЃЉгыБъМлгІИЖПюН№ЖюxЃЈЕЅЮЛЃКдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() ЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЁАВннЎНкЁБЦкМфЃЌШчКЮбЁдёМзЁЂввСНМвЫЎЙћЕъЙКТђВннЎИќЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌ![]() ЮЊОиаЮ
ЮЊОиаЮ![]() ЕФБп
ЕФБп![]() ЩЯвЛЕуЃЌЖЏЕу
ЩЯвЛЕуЃЌЖЏЕу![]() ЭЌЪБДгЕу
ЭЌЪБДгЕу![]() ГіЗЂЃЌЕу
ГіЗЂЃЌЕу![]() биелЯп
биелЯп![]() дЫЖЏЕНЕу
дЫЖЏЕНЕу![]() ЪБЭЃжЙЃЌЕу
ЪБЭЃжЙЃЌЕу![]() би
би![]() дЫЖЏЕНЕу
дЫЖЏЕНЕу![]() ЪБЭЃжЙЃЌЫќУЧдЫЖЏЕФЫйЖШЖМЪЧ
ЪБЭЃжЙЃЌЫќУЧдЫЖЏЕФЫйЖШЖМЪЧ![]() УыЃЎЩш
УыЃЎЩш![]() ЭЌЪБГіЗЂ
ЭЌЪБГіЗЂ![]() УыЪБЃЌ
УыЪБЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌвбжЊ
ЃЌвбжЊ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМ2ЫљЪОЃЎЧыЛиД№ЃК
ЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМ2ЫљЪОЃЎЧыЛиД№ЃК
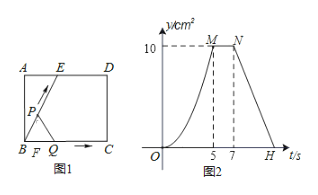
ЃЈ1ЃЉЯпЖЮ![]() ЕФГЄЮЊ_______cmЃЛ
ЕФГЄЮЊ_______cmЃЛ
ЃЈ2ЃЉЕБдЫЖЏЪБМф![]() УыЪБЃЌ
УыЪБЃЌ![]() жЎМфЕФОрРыЪЧ_______
жЎМфЕФОрРыЪЧ_______![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
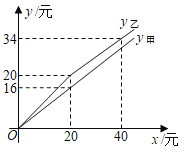
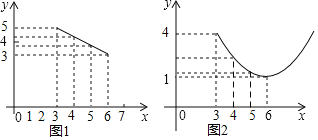
ЁОЬтФПЁПФГжжЪпВЫУПЧЇПЫЪлМлy1ЃЈдЊЃЉгыЯњЪлдТЗнxжЎМфЕФЙиЯЕШчЭМ1ЫљЪОЃЌУПЧЇПЫГЩБОy2ЃЈдЊЃЉгыЯњЪлдТЗнxжЎМфЕФЙиЯЕШчЭМ2ЫљЪОЃЌЦфжаЭМ1жаЕФЕудкЭЌвЛЬѕЯпЖЮЩЯЃЌЭМ2жаЕФЕудкЖдГЦжсЦНаагкyжсЕФЭЌвЛЬѕХзЮяЯпЩЯЃЌЧвХзЮяЯпЕФзюЕЭЕуЕФзјБъЮЊ(6ЃЌ1)ЃЎ
ЃЈ1ЃЉЧѓГіy1гыxКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓГіy2гыxКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЩшетжжЪпВЫУПЧЇПЫЪевцЮЊwдЊЃЌЪдЮЪдкФФИідТЗнГіЪлетжжЪпВЫЃЌwНЋШЁЕУзюДѓжЕЃПВЂЧѓГіДЫзюДѓжЕЃЎЃЈЪевцЃНЪлМлЉГЩБОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧГЃЪ§ЃЌ
ЪЧГЃЪ§ЃЌ![]() ЃЉЕФЭМЯѓЕФвЛВПЗжгы
ЃЉЕФЭМЯѓЕФвЛВПЗжгы![]() жсЕФНЛЕу
жсЕФНЛЕу![]() дк
дк![]() гы
гы![]() жЎМфЃЌЖдГЦжсЮЊжБЯп
жЎМфЃЌЖдГЦжсЮЊжБЯп![]() .ЯТСаНсТлЃКЂй
.ЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЈ
ЃЈ![]() ЮЊЪЕЪ§ЃЉЃЛЂнЕБ
ЮЊЪЕЪ§ЃЉЃЛЂнЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .ЦфжаЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
.ЦфжаЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
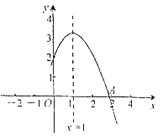
A. 2B. 3C. 4D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌ![]() ЃЌ
ЃЌ![]() ЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
 ЁЁЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁЁЁ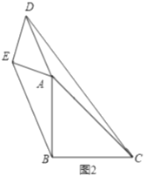
ЃЈ1ЃЉШчЙћ![]() ЃЛ
ЃЛ
ЂйЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкШє![]() ЃЌ
ЃЌ![]() ЪЧЙигк
ЪЧЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЕФСНИљЃЌЧѓ
ЕФСНИљЃЌЧѓ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЎ
ЃЎ
Ђйдк![]() ЩЯЗНЃЌгы
ЩЯЗНЃЌгы![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЭЌвЛЦНУцФкеввЛЕу
ЭЌвЛЦНУцФкеввЛЕу![]() ЃЌЪЙЫФБпаЮ
ЃЌЪЙЫФБпаЮ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЫФБпаЮ
ЫФБпаЮ![]() гыЫФБпаЮ
гыЫФБпаЮ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЫФБпаЮ
ЫФБпаЮ![]() ЯрЕШЃЌВЂМђвЊЫЕУїбАевЕу
ЯрЕШЃЌВЂМђвЊЫЕУїбАевЕу![]() ЕФзїЗЈЃЛ
ЕФзїЗЈЃЛ
ЂкШє![]() ЫФБпаЮ
ЫФБпаЮ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФГЄ ЃЎ
ЕФГЄ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦћГЕЯњЪлЙЋЫОвЛЮЛЯњЪлОРэ1ЁЊ5дТЗнЕФЦћГЕЯњЪлЭГМЦЭМШчЯТЃК
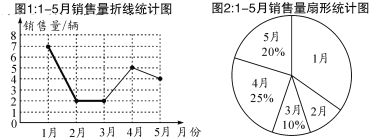
ЃЈ1ЃЉвбжЊ1дТЕФЯњЪлСПЪЧ2дТЕФЯњЪлСПЕФ3.5БЖЃЌдђ1дТЕФЯњЪлСПЮЊ________СОЃЌдкЩШаЮЭМжаЃЌ2дТЕФЯњЪлСПЫљЖдгІЕФЩШаЮЕФдВаФНЧДѓаЁЮЊ________ЃЛ
ЃЈ2ЃЉВЙШЋЭМжаЯњЪлСПелЯпЭГМЦЭМЃЛ
ЃЈ3ЃЉвбжЊ4дТЗнЯњЪлЕФГЕжага3СОЙњВњГЕКЭ2СОКЯзЪГЕЃЌЙњВњГЕЗжБ№гУG1ЃЌG2ЃЌG3БэЪОЃЌКЯзЪГЕЗжБ№гУH1ЃЌH2БэЪОЃЌЯжДгет5СОГЕжаЫцЛњГщШЁСНСОГЕВЮМгЙЋЫОЕФЛиРЁЛюЖЏЃЌЧыгУСаОйЗЈЃЈЛЪїзДЭМЛђСаБэЃЉЧѓГіЁАГщЕНЕФСНСОГЕЖМЪЧЙњВњГЕЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
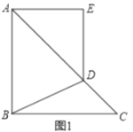
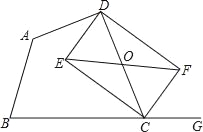
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЫФБпаЮABCDжаЃЌЕуGдкБпBCЕФбгГЄЯпЩЯЃЌCEЦНЗжЁЯBCDЃЌCFЦНЗжЁЯGCDЃЌEFЁЮBCНЛCDгкЕуOЃЎ
ЃЈ1ЃЉЧѓжЄЃКOE=OFЃЛ
ЃЈ2ЃЉШєЕуOЮЊCDЕФжаЕуЃЌЧѓжЄЃКЫФБпаЮDECFЪЧОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌABCDжаЃЌADЃН5ЃЌABЃН3ЃЎШєMЮЊЩфЯпADЩЯЕФвЛИіЖЏЕуЃЌНЋЁїABMбиBMелЕўЕУЕНЁїNBMЃЎШєЁїNBCЪЧжБНЧШ§НЧаЮЃЎдђЫљгаЗћКЯЬѕМўЕФMЕуЫљЖдгІЕФAMГЄЖШЕФКЭЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com