
 已知二次函数y=x2-(2k+1)x+k2+k(k>0)
已知二次函数y=x2-(2k+1)x+k2+k(k>0)分析 (1)直接将k的值代入函数解析式,进而利用配方法求出顶点坐标;
(2)利用根的判别式得出△=1,进而得出答案;
(3)根据题意首先表示出Q点坐标,以及表示出OA,AB的长,再利用两点之间距离求出AQ的长,进而求出答案.
解答 解:(1)将k=$\frac{1}{2}$代入二次函数可求得,
y=x2-2x+$\frac{3}{4}$
=(x-1)2-$\frac{1}{4}$,
故抛物线的顶点坐标为:(1,-$\frac{1}{4}$);
(2)∵一元二次方程x2-(2k+1)x+k2+k=0,
∴△=b2-4ac=[-(2k+1)]2-4(k2+k)=1>0,
∴关于x的一元二次方程x2-(2k+1)x+k2+k=0有两个不相等的实数根;
(3)由题意可得:点P的坐标为(0,-1),
则0=x2-(2k+1)x+k2+k
0=(x-k-1)(x-k),
故A(k,0),B(k+1,0),
当x=0,则y=k2+k,
故C(0,k2+k)
则AB=k+1-k=1,OA=k,
可得
${y_{PA}}=\frac{1}{k}x-1$,
yBC=-kx+k2+k,
当$\frac{1}{k}$x-1=-kx+k2+k,
解得:x=k+$\frac{{k}^{2}}{{k}^{2}+1}$,
则代入原式可得:y=$\frac{k}{{k}^{2}+1}$,
则点Q坐标为$(k+\frac{k^2}{{{k^2}+1}},\frac{k}{{{k^2}+1}})$
运用距离公式得:AQ2=($\frac{{k}^{2}}{{k}^{2}+1}$)2+($\frac{k}{{k}^{2}+1}$)2=$\frac{{k}^{2}}{{k}^{2}+1}$,
则OA2=k2,AB2=1,
故$\frac{1}{O{A}^{2}}$+$\frac{1}{A{B}^{2}}$=$\frac{1}{{k}^{2}}$+1=$\frac{1+{k}^{2}}{{k}^{2}}$=$\frac{1}{A{Q}^{2}}$,
则$\frac{1}{{O{A^2}}}+\frac{1}{{A{B^2}}}=\frac{1}{{A{Q^2}}}$.
点评 此题主要考查了二次函数综合以及根的判别式和配方法求二次函数顶点坐标和两点之间距离求法等知识,正确表示出Q点坐标是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B
如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
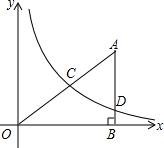 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.30 | B. | 0.31 | C. | 0.32 | D. | 0.33 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com