解:(1)通过图象观察和题意EA、HD、GC、FB分别是方砖TPQR四边的中垂线,且四边形HEFG是正方形就可以得出方砖TPQR面上的图案是轴对称图形,又是中心对称图形.
(2)设小沟槽EA的长是xcm,则EG的长度为24-2x.
∵四边形HEFG是正方形,
∴HE=HG,∠GHE=90°,
∴HE
2+HG
2=EG
2.
∴2HE
2=(24-2x)
2,
∴HE
2=2x
2-48x+288.
∵
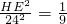
,
∴
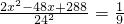
,
解得:x
1=12+4

(舍去),x
2=12-4

.
∴EA=12-4

.
故答案为:C.
分析:(1)由图象和题意可以得出方砖TPQR面上的图案是轴对称图形,又是中心对称图形;
(2)设小沟槽EA的长是xcm,则EG的长度为24-2x,由勾股定理就可以表示出HE,由相似形的面积比等于相似比的平方建立方程求出其解即可.
点评:本题考查了一元二次方程的运用,轴对称图象的运用,中心对称图象的运用,相似形的性质的运用,解答时运用相似图形的性质建立建立方程是关键.

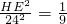 ,
,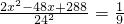 ,
, (舍去),x2=12-4
(舍去),x2=12-4 .
. .
.

 名校课堂系列答案
名校课堂系列答案