
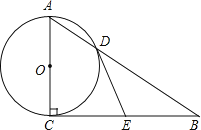
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.
【答案】(1)详见解析;(2)①3![]() ;②45.
;②45.
【解析】
(1)证出EC为⊙O的切线;由切线长定理得出EC=ED,再求得EB=ED,即可得出结论;
(2)①由含30°角的直角三角形的性质得出AB,由勾股定理求出BC,再根据BD=BCcos30°计算即可;
②由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°,然后根据有一组邻边相等的矩形是正方形,即可得到结论.
(1)证明:连接DO.
∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴BE=ED,
∴BE=EC;
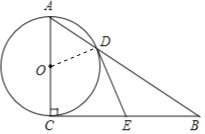
(2)解:①∵∠ACB=90°,∠B=30°,AC=2![]() ,
,
∴AB=2AC=4![]() ,
,
∴BC=![]() ,
,
∵AC为直径,
∴∠BDC=∠ADC=90°,
∴BD=BCcos30°=3![]()
故答案为:3![]() ;
;
②当∠B=45°时,四边形ODEC是正方形,
理由如下:
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:

(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
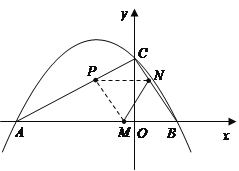
【题目】如图,二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .连结
.连结![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,且当
,且当![]() 和
和![]() 时二次函数的函数值
时二次函数的函数值![]() 相等.
相等.
(1)求实数![]() 的值;
的值;
(2)若点![]() 同时从
同时从![]() 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿![]() 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为
边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为![]() 秒时,连结
秒时,连结![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 点恰好落在
点恰好落在![]() 边上的
边上的![]() 处,求
处,求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(3)在(2)的条件下,二次函数图象的对称轴上是否存在点![]() ,使得以
,使得以![]() 为项点的三角形与
为项点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
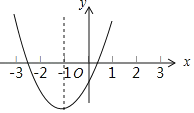
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a﹣b+c<0;⑤3a+c>0.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
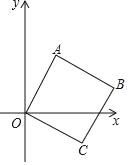
【题目】如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A. (![]() ,-1) B. (2,﹣1) C. (1,-
,-1) B. (2,﹣1) C. (1,-![]() ) D. (﹣1,
) D. (﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
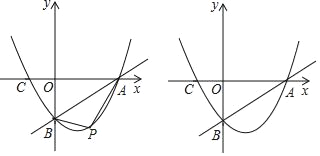
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用黑白棋子摆出下列一组图形,根据规律可知.
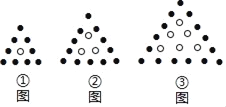
(1)在第n个图中,白棋共有 枚,黑棋共有 枚;
(2)在第几个图形中,白棋共有300枚;
(3)白棋的个数能否与黑棋的个数相等?若能,求出是第几个图形,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算,请阅读以下材料,并完成相应的问题.
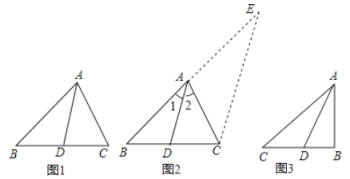
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则![]() =
=![]() .下面是这个定理的部分证明过程.
.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com