练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．比$\sqrt{5}$大的数是（　　）
    A．1B．$\sqrt{3}$C．2D．$\frac{5}{2}$

    分析 根据二次根式的性质进行比较即可．

    解答 解：1＜$\sqrt{5}$，A错误；
    $\sqrt{3}$＜$\sqrt{5}$，B错误；
    2＜$\sqrt{5}$，C错误；
    $\frac{5}{2}$＞$\sqrt{5}$，D正确，
    故选：D．

    点评 本题考查的是实数的大小比较，掌握二次根式的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求代数式$\frac{a+1}{a}$÷（a-$\frac{1+2a^2}{3a}$）的值，再选取一个合适的a值代入计算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

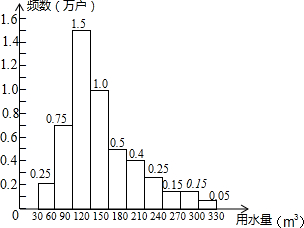    6．为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m3），绘制了统计图．如图所示，下面四个推断合理的是（　　）
    ①年用水量不超过180m3的该市居民家庭按第一档水价交费；
    ②年用水量超过240m3的该市居民家庭按第三档水价交费；
    ③该市居民家庭年用水量的中位数在150-180之间；
    ④该市居民家庭年用水量的平均数不超过180．
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．分解因式3m4-48=3（m2+4）（m+2）（m-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图1，在平面直角坐标系中，点B在x轴正半轴上，OB的长度为2m，以OB为边向上作等边三角形AOB，抛物线l：y=ax2+bx+c经过点O，A，B三点
    （1）当m=2时，a=-$\frac{\sqrt{3}}{2}$，当m=3时，a=-$\frac{\sqrt{3}}{3}$；
    （2）根据（1）中的结果，猜想a与m的关系，并证明你的结论；
    （3）如图2，在图1的基础上，作x轴的平行线交抛物线l于P、Q两点，PQ的长度为2n，当△APQ为等腰直角三角形时，a和n的关系式为a=-$\frac{1}{n}$；
    （4）利用（2）（3）中的结论，求△AOB与△APQ的面积比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．化简求值：$\frac{a}{{a}^{2}-4}$•$\frac{a+2}{{a}^{2}-3a}$-$\frac{1}{2-a}$，其中a=$\sqrt{2}$+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．若点P（m，n）在直角坐标系的第二象限，则一次函数y=mx+n的大致图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE=3，若平行四边形ABCD的周长是16，则EC等于2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件．已知生产1件A种产品需甲种原料9千克，乙种原料3千克，可获利700元；生产1件B种产品需甲种原料4千克，乙种原料10千克，可获利1200元．设生产A、B两种产品可获总利润是y元，其中A种产品的生产件数是x．
    （1）写出y与x之间的函数关系式；
    （2）符合题意的生产方案有几种？请你帮忙设计出来；
    （3）如何安排A、B两种产品的生产件数，使总利润y有最大值，并求出y的最大值．

    查看答案和解析>>

    同步练习册答案