Question

20．如图，四边形ABCD中，E、F、G、H依次是各边的中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为5、6、7，试求四边形DHOG的面积．

Answer 1

分析 连接OC，OB，OA，OD，易证S_△OBF=S_△OCF，S_△ODG=S_△OCG，S_△ODH=S_△OAH，S_△OAE=S_△OBE，所以S_{四边形AEOH}+S_{四边形CGOF}=S_{四边形DHOG}+S_{四边形BFOE}，所以可以求出S_{四边形DHOG}．

解答 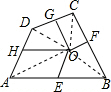解：连接OC，OB，OA，OD，
∵E、F、G、H依次是各边中点，
∴△AOE和△BOE等底等高，
∴S_△OAE=S_△OBE，
同理可证，S_△OBF=S_△OCF，S_△ODG=S_△OCG，S_△ODH=S_△OAH，
∴S_{四边形AEOH}+S_{四边形CGOF}=S_{四边形DHOG}+S_{四边形BFOE}，
∵S_{四边形AEOH}=5，S_{四边形BFOE}=6，S_{四边形CGOF}=7，
∴5+7=6+S_{四边形DHOG}，
解得：S_{四边形DHOG}=6．

点评 本题考查了中点四边形、三角形的面积．解决本题的关键将各个四边形划分，充分利用给出的中点这个条件，证得三角形的面积相等，进而证得结论．