
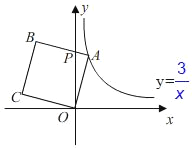
【题目】如图,点A在反比例函数y=![]() (x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.
(x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.
 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=3,BC=4,动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q的运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止运动,连接PQ,设它们的运动时间为t(t>0)秒.

(1)设△CBQ的面积为S,请用含有t的代数式来表示S;
(2)线段PQ的垂直平分线记为直线l,当直线l经过点C时,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青少年是祖国的未来,增强青少年体质,促进青少年健康成长,是关系国家和民族未来的大事,为了响应“足球进校园”的号召,我市某中学准备购买一批足球,若购买2个A品牌足球和3个B品牌足球共需340元;购买5个A品牌足球和2个B品牌足球共需410元.
(1)购买一个A品牌足球,一个B品牌足球各需多少元?
(2)根据学校的实际情况,需购买两种品牌足球共50个,并且总费用不超过3120元,问最多可以购买多少个B品牌足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人以各自的交通工具、相同路线,前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②乙走了8km后遇到甲;③乙出发6分钟后追上甲;④甲走了28分钟时,甲乙相距3km.其中正确的是( )

A. 只有① B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=kx+b 经过点A(﹣![]() ,0)和点B(2,5).
,0)和点B(2,5).
(1)求直线l1与y轴的交点坐标;
(2)若点C(a,a+2)与点D在直线l1上,过点D的直线l2与x轴正半轴交于点 E,当AC=CD=CE 时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )

A. 点B到AO的距离为sin54°
B. 点A到OC的距离为sin36°sin54°
C. 点B到AO的距离为tan36°
D. 点A到OC的距离为cos36°sin54°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )
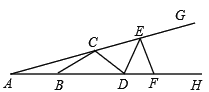
A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com