【题目】如图，湿地景区岸边有三个观景台
、
、
.已知
m， 
m，点
位于点
的南偏西60. 7°方向，点
位于点
的南偏东66. 1°方向.
(1)求
的面积;
(2)景区规划在线段
的中点
处修建一个湖心亭，并修建观景栈道
.试求
、
间的距离.(结果精确到0. 1 m，参考数据: 
， 
, 
， 
， 
， 
， 
)
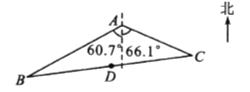
【答案】（1）560000（2）565.6
【解析】试题分析：（1）作CE⊥BA于E．在Rt△ACE中，求出CE即可解决问题；
（2）接AD，作DF⊥AB于F，则DF∥CE．首先求出DF、AF，再在Rt△ADF中求出AD即可．
试题解析：解：（1）作CE⊥BA于E．在Rt△AEC中，∠CAE=180°﹣60.7°﹣66.1°=53.2°，∴CE=ACsin53.2°≈1000×0.8=800米，∴S△ABC=
ABCE=
×1400×800=560000平方米．
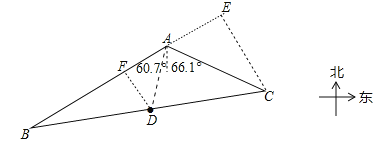
（2）连接AD，作DF⊥AB于F，则DF∥CE．∵BD=CD，DF∥CE，∴BF=EF，∴DF=
CE=400米．∵AE=ACcos53.2°≈600米，∴BE=AB+AE=2000米，∴AF=
EB﹣AE=400米．在Rt△ADF中，AD=
=400
=565.6米．
春雨教育同步作文系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y=x2在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为A1，A2，A3…An，…．将抛物线y=x2沿直线L：y=x向上平移，得一系列抛物线，且满足下列条件：①抛物线的顶点M1，M2，M3，…Mn，…都在直线L：y=x上；②抛物线依次经过点A1，A2，A3…An，…．则顶点M2014的坐标为_______．
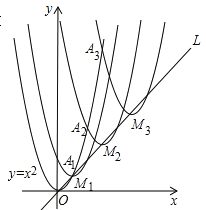
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知y关于x的二次函数：y=
（m﹣n）x2+nx+t﹣n．
（1）当m=t=0时，判断该函数图象和x轴的交点个数；
（2）若n=t=3m，当x为何值时，函数有最值；
（3）是否存在实数m和t，使该函数图象和x轴有交点，且n的最大值和最小值分别为8和4？若存在，求m和t值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
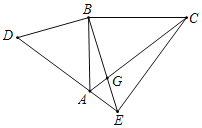
【题目】如图，已知Rt△ABC中，两条直角边AB=3，BC=4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则△BEC的面积=__________________
查看答案和解析>>
科目：初中数学 来源： 题型：
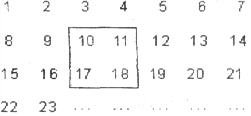
【题目】把正整数1，2，3，4，……，2009排列成如图所示的一个表
（1）用一正方形在表中随意框住4个数，把其中最小的数记为x，另三个数用含x的式子表示出来，从小到大依次是 ， ， 。
（2）当被框住的4个数之和等于416时，x的值是多少?
（3）被框住的4个数之和能否等于622？如果能，请求出此时x的值；如果不能，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
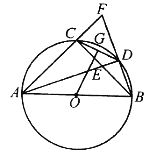
【题目】如图， 
内接于⊙
， 
， 
的平分线
与⊙
交于点
，与
交于点
，延长
，与
的延长线交于点
，连接
， 
是
的中点，连接
.
(1)判断
与
的位置关系，写出你的结论并证明;
(2)求证: 
;
(3)若
，求⊙
的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
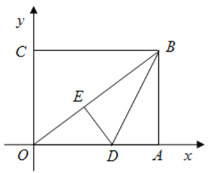
【题目】如图，在平面直角坐标系中，
为坐标原点，矩形
的顶点
、
，将矩形的一个角沿直线
折叠，使得点
落在对角线
上的点
处，折痕与
轴交于点
．
（1）求线段的长度；
（2）求直线所对应的函数表达式；
（3）若点
在线段上，在线段
上是否存在点
，使以
为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．
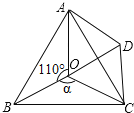
（1）求证：△COD是等边三角形；
（2）当a=150°时，试判断△AOD的形状，并说明理由；
（3）探究：当a为多少度时，△AOD是等腰三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
的部分图象如图，图象过点（﹣1，0），对称轴为直线
，下列结论：①
；②
；③
；④当
时， 
随
的增大而增大．其中正确的结论有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com