
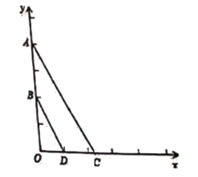
【题目】已知:如图,平面直角坐标系中,![]() ,
,![]() ,点C是x轴上一点,点D为OC的中点.
,点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于2,求点C的坐标;
(3)如果![]() 于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
【答案】(1)BD∥AC;(2) ;(3)
;(3)![]()
【解析】
(1)由A与B的坐标求出OA与OB的长,进而得到B为OA的中点,而D为OC的中点,利用中位线定理即可得证;
(2)如图1,作BF⊥AC于点F,取AB的中点G,确定出G坐标,由平行线间的距离相等求出BF的长,在直角三角形ABF中,利用斜边上的中线等于斜边的一半求出FG的长,进而确定出三角形BFG为等边三角形,即∠BAC=30°,设OC=x,则有AC=2x,利用勾股定理表示出OA,根据OA的长求出x的值,即可确定出C坐标;
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,进而得到DE垂直于OC,再由D为OC中点,得到OE=CE,再由OE垂直于AC,得到三角形AOC为等腰直角三角形,求出OC的长,确定出C坐标,设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出AC解析式.
(1)![]() ,
,![]() ,
,
![]() ,
,![]() ,点B为线段OA的中点,
,点B为线段OA的中点,
![]() 点D为OC的中点,即BD为
点D为OC的中点,即BD为![]() 的中位线,
的中位线,
![]() ;
;
(2)如图1,作![]() 于点F,取AB的中点G,则
于点F,取AB的中点G,则![]() ,
,
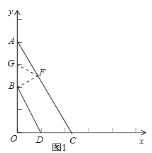
![]() ,BD与AC的距离等于2,
,BD与AC的距离等于2,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,点G为AB的中点,
,点G为AB的中点,
![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() .
.
![]() ,
,
设![]() ,则
,则![]() ,
,
根据勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 点C在x轴的正半轴上,
点C在x轴的正半轴上,
![]() 点C的坐标为
点C的坐标为 ;
;
(3)如图2,当四边形ABDE为平行四边形时,![]() ,
,

![]() ,
,
![]() 点D为OC的中点,
点D为OC的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点C在x轴的正半轴上,
点C在x轴的正半轴上,
![]() 点C的坐标为
点C的坐标为![]() ,
,
设直线AC的解析式为![]() .
.
将![]() ,
,![]() 得
得
![]() ,
,
解得:![]() .
.
![]() 直线AC的解析式为
直线AC的解析式为![]() .
.


科目:初中数学 来源: 题型:
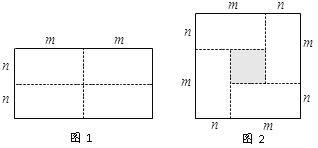
【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的方法拼成一个边长为(m+n)的正方形.
⑴ 请用两种不同的方法求图2中阴影部分的面积.
方法1: ;方法2: ;
⑵ 观察图2写出![]() ,
,![]() ,
,![]() 三个代数式之间的等量关系: ;
三个代数式之间的等量关系: ;
⑶ 根据⑵中你发现的等量关系,解决如下问题:若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
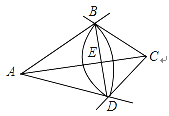
【题目】如图,在![]() 中,按如下步骤作图:
中,按如下步骤作图:
①以点A为圆心,AB长为半径画弧;
②以点C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD、CD;
(1)求证:![]() ;
;
(2)当![]() 时,猜想四边形ABCD是什么四边形,并证明你的结论;
时,猜想四边形ABCD是什么四边形,并证明你的结论;
(3)当![]() ,
,![]() ,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有20箱苹果,以每箱25千克为标准,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如表:
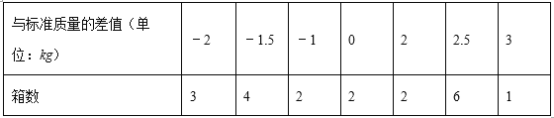
(1)20箱苹果中,最重的一箱比最轻的一箱重 kg;
(2)与标准质量相比,20箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价12元,则售出这20箱苹果可获得多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列数:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这串数是由小明按照一定规则写下来的,他第一次写下“
这串数是由小明按照一定规则写下来的,他第一次写下“![]() ,
,![]() ”,第二次接着写“
”,第二次接着写“![]() ,
,![]() ”,第三次接着写“
”,第三次接着写“![]() ,
,![]() ”,第四次接着写“
”,第四次接着写“![]() ,
,![]() ”,沿着这个规则,那么接着“
”,沿着这个规则,那么接着“![]() ,
,![]() ”后面的三个数应为( )
”后面的三个数应为( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市城市居民用电收费方式有以下两种:
(甲)普通电价:全天0.53元/度;
(乙)峰谷电价:峰时(早8:00~晚21:00)0.56元/度;谷时(晚21:00~早8:00)0.36元/度.
估计小明家下月总用电量为200度,
⑴若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
⑵请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
⑶到下月付费时, 小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com