
 ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数 的零点。
的零点。 (
( m为常数)。
m为常数)。 =0时,求该函数的零点;
=0时,求该函数的零点; 取何值,该函数总有两个零点;
取何值,该函数总有两个零点; 和
和 ,且
,且 ,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线
,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。 和
和 (2)证明见解析(3)
(2)证明见解析(3)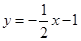
 =0时,该函数的零点为
=0时,该函数的零点为 和
和 。 ……………………………2分
。 ……………………………2分
 取何值,方程
取何值,方程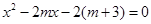 总有两个不相等的实数根。
总有两个不相等的实数根。 取何值,该函数总有两个零点。 ………………………………6分
取何值,该函数总有两个零点。 ………………………………6分 ,
,
 解得
解得 。
。 。 ………………………………8分
。 ………………………………8分
 ),B(4,0)
),B(4,0) 的对称点B’,连结AB’,
的对称点B’,连结AB’, 的交点就是满足条件的M点。 ………………………………10分
的交点就是满足条件的M点。 ………………………………10分 与x轴、y轴的交点分别为C(10,0),D(0,10)。
与x轴、y轴的交点分别为C(10,0),D(0,10)。
 ) ………………………………12分
) ………………………………12分 ,则
,则 ,解得
,解得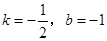
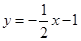 ,
,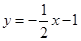 。 ………………………………14分
。 ………………………………14分

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:不详 题型:单选题
 ,DE的延长线交CB的延长线于点F,设CF=
,DE的延长线交CB的延长线于点F,设CF=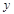 ,则下列图象能正确反映
,则下列图象能正确反映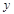 与
与 的函数关系的是( )
的函数关系的是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com