
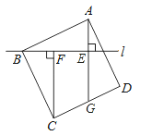
【题目】如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
【答案】(1)证明见解析;(2)115°.
【解析】
试题(1)根据正方形的性质,易得△ABE与△BCF的两角与一条边相等,利用全等三角形的判定条件AAS,可证明两三角形全等;(2)根据△ABE≌△BCF,又知∠CBF=65°,可得∠BAE=65°,又由正方形的性质可得AB∥DC,即可得出∠AGC的度数.
试题解析:解:(1)证明:∵正方形ABCD,

∴AB=CB,∠ABC=90° (1分)
∵AE![]() 于点E,
于点E,
∴∠ABE+∠BAE=90°, (2分)
∴∠BAE=∠CBF. (3分)
又∵∠AEB=∠BFC=90°, (4分)
∴△ABE≌△BCF(AAS). (5分)
(2)∵△ABE≌△BCF,∠CBF=65°,
∴∠BAE=65°, (6分)
又由正方形ABCD得AB∥DC, (7分)
∴∠AGC=115°. (8分)


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
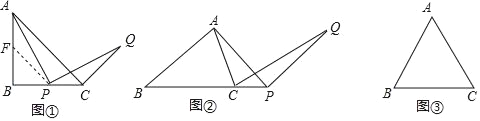
【题目】在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B,C重合),连接AP,将线段PA绕点P顺时针旋转α度得到线段PQ,连接CQ.
(1)当α=90°,且点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图1,图中与△APF全等的是哪个三角形,∠ACQ的度数.
(2)当点P在BC延长线上,AB:AC=m:n时,如图2,试求线段BP与CQ的比值;
(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其他活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.

请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了__________名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为__________,喜欢“戏曲”活动项目的人数是__________人;
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
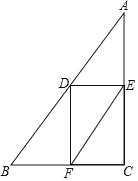
【题目】如图,在△ABC中,∠C=90°,点D是边AB上的动点,过点D作DE∥BC交AC于E,过E作EF∥AB交BC于F,连结DF.
(1)若点D是AB的中点,证明:四边形DFEA是平行四边形;
(2)若AC=8,BC=6,直接写出当△DEF为直角三角形时AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
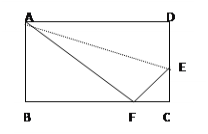
【题目】如图,矩形ABCD中,折叠矩形一边AD,使点D落在BC边的点F处,已知折痕AE=![]() ,且CE:CF=3:4,则矩形ABCD的周长为()
,且CE:CF=3:4,则矩形ABCD的周长为()
A. 36cm B. 3![]() C. 72cm D. 7
C. 72cm D. 7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于同一锐角α有:sin2α+cos2α=1,现锐角A满足sinA+cosA=![]() .
.
试求:(1)sinAcosA的值;(2)sinA﹣cosA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
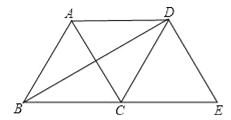
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
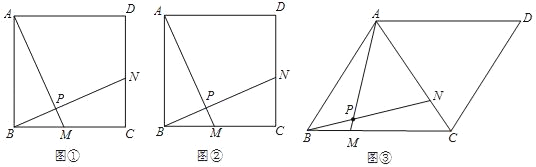
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:
(1)这个班有多少人参加了本次数学调研考试?
(2)60.5~70.5分数段的频数和频率各是多少?
(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com