
【题目】可以用如下方法求方程x2-2x-2=0的实数根的范围:利用函数y=x2-2x-2的图象可知,当x=0时,y<0,当x=-1时,y>0,所以方程有一个根在-1和0之间.
(1)参考上面的方法,求方程x2-2x-2=0的另一个根在哪两个连续整数之间;
(2)若方程x2-2x+c=0有一个根在0和1之间,求c的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
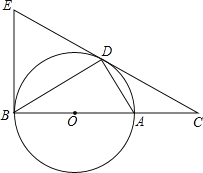
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
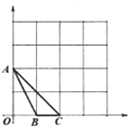
【题目】如图,在下列![]() (边长为1)的网格中,已知
(边长为1)的网格中,已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 在格点上,请分别按不同要求在网格中描出一个格点
在格点上,请分别按不同要求在网格中描出一个格点![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(1)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后所得的三角形,点
,画出旋转后所得的三角形,点![]() 旋转后落点为
旋转后落点为![]() .
.
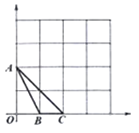
(2)经过![]() ,
,![]() ,
,![]() 三点有一条抛物线,请找到点
三点有一条抛物线,请找到点![]() ,使点
,使点![]() 也落在这条抛物线上.
也落在这条抛物线上.
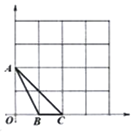
(3)经过![]() ,
,![]() ,
,![]() 三点有一个圆,请找到一个横坐标为2的点
三点有一个圆,请找到一个横坐标为2的点![]() ,使点
,使点![]() 也落在这个圆上.
也落在这个圆上.
(1)点![]() 的坐标为( , )
的坐标为( , )
(2)点![]() 的坐标为( , )/span>
的坐标为( , )/span>
(3)点![]() 的坐标为( , )
的坐标为( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
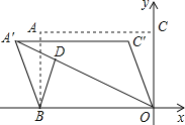
【题目】如图,在平面直角坐标系中,矩形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,AC长为![]() ,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=
,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=![]() 的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A(-1,0),点B,与y轴交于点C(0,-3),作直线BC.点P是抛物线的对称轴上的一个动点,P点到x轴和直线BC的距离分别为PD、PE.
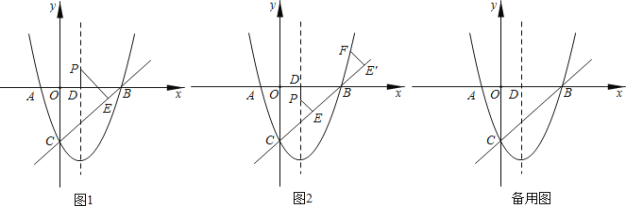
(1)求抛物线解析式;
(2)当P点运动过程中满足PE=PD时,求此时点P的坐标;
(3)如图2,从点B处沿着直线BC的垂线翻折PE得到FE',当点F在抛物线上时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线y=-(x-a)(x-4)(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
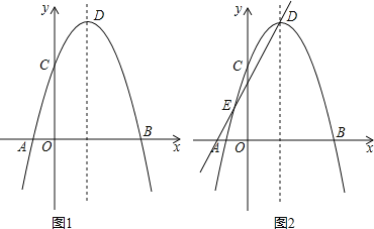
(1)若D点坐标为(![]() ),求抛物线的解析式和点C的坐标;
),求抛物线的解析式和点C的坐标;
(2)若点M为抛物线对称轴上一点,且点M的纵坐标为a,点N为抛物线在x轴上方一点,若以C、B、M、N为顶点的四边形为平行四边形时,求a的值;
(3)直线y=2x+b与(1)中的抛物线交于点D、E(如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为D′,与直线的另一个交点为E′,与x轴的交点为B′,在平移的过程中,求D′E′的长度;当∠E′D′B′=90°时,求点B′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,用尺规作图的方法作出射线AD和直线EF,设AD交EF于点O,连结BE、OC.下列结论中,不一定成立的是( )

A.AE⊥BEB.EF平分∠AEBC.OA=OCD.AB=BE+EC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com