
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计算;月用水量超过20
计算;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 计算,超过部分按2.6元/
计算,超过部分按2.6元/![]() 计算. 设某户家庭月用水量
计算. 设某户家庭月用水量![]()
![]() .
.

(1)用含![]() 的式子表示:
的式子表示:
当0≤![]() ≤20时,水费为 元;
≤20时,水费为 元;
当![]() >20时,水费为 元.
>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
【答案】(1)2x,(2.6x-12);(2)小花家这个季度共缴纳水费114.4元.
【解析】试题分析:(1)根据水费=单价×数量计算即可;当0≤![]() ≤20时,水费为2x元;当
≤20时,水费为2x元;当![]() >20时,
>20时,
水费为2×20+2.6(x-20);
(2)因4、5月份用水量不超过20m3,所以代入2x求值;因5月份用水量超过20m3,所以代入2.6x-12求值,然后把三个月的水费相加.
解:(1)当0≤![]() ≤20时,水费为 2x___元;
≤20时,水费为 2x___元;
当![]() >20时,水费为 (2.6x-12)__元.
>20时,水费为 (2.6x-12)__元.
(2)15×2+17×2+2.6×24-12= 30+34+62.4-12= 114.4 ,
答:小花家这个季度共缴纳水费114.4元.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】近年来,各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15﹣65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A:没影响;B:影响不大;C:有影响,建议做无声运动,D:影响很大,建议取缔;E:不关心这个问题,将调查结果绘统计整理并绘制成如下两幅不完整的统计图.

请根据以上信息解答下列问题:
(1)填空m=________,态度为C所对应的圆心角的度数为________;
(2)补全条形统计图;
(3)若全区15﹣65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
(4)若在这次调查的市民中,从态度为A的市民中抽取一人的年龄恰好在年龄段15﹣35岁的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果有4个不同的正整数a、b、c、d满足(2019﹣a)(2019﹣b)(2019﹣c)(2019﹣d)=9,那么a+b+c+d的值为( )
A. 0B. 9C. 8048D. 8076
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
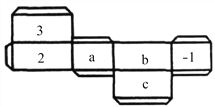
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)+4abc].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AD是菱形AEDF的一条对角线,且点E在矩形ABCD的边BC上.
(1)求证:△ABE≌△DCE;
(2)直接写出当矩形边长AD与AB之间满足什么关系时,菱形AEDF为正方形.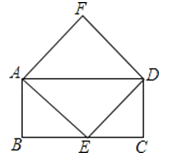
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com