
【题目】大黄鱼是中国特有的地方性鱼类,有“国鱼”之称,由于过去滥捕等多种因素,大黄鱼资源已基本枯竭,目前,我市已培育出十余种大黄鱼品种,某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广,通过实验得知“甬岱”品种鱼苗成活率为![]() ,并把实验数据绘制成下列两幅统计图(部分信息未给出):
,并把实验数据绘制成下列两幅统计图(部分信息未给出):
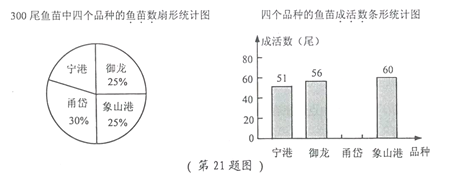
(1) 求实验中“宁港”品种鱼苗的数量;
(2) 求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
【答案】(1)60尾.(2)72尾;补图见解析;(3)选“宁港”品种进行推广.
【解析】
试题分析:(1)先求出“宁港”品种鱼苗数的百分比,再乘以300即可得解;
(2)根据实验中“甬岱”品种鱼苗数的百分比和成活率即可计算出结果;然后补全图形即可;
(3)通过计算、分析成活率即可选择推广品种.
试题解析:(1)300×(1-30%-25%-25%)=60(尾)
答:实验中“宁港”品种鱼苗有60尾.
(2)300×30%×80%=72(尾)
答:实验中“甬岱”品种鱼苗有72尾成活.
补全条形统计图如图所示:
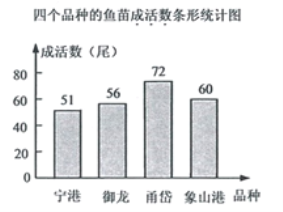
(3) “宁港”品种鱼苗的成活率为![]() ×100%=85%;
×100%=85%;
“御龙”品种鱼苗的成活率为![]() ×100%=74.6%;
×100%=74.6%;
“象山港”品种鱼苗的成活率为![]() ×100%=80%;
×100%=80%;
答:“宁港”品种鱼苗的成活率最高,应选“宁港”品种进行推广.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:

(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家发改委已于2012年5月24日核准广东湛江钢铁基地项目,项目由宝钢湛江钢铁有限公司投资建设,预计投产后年产10200000吨钢铁,数据10200000用科学记数法表示为( )
A.102×105
B.10.2×106
C.1.02×106
D.1.02×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线l:y=﹣ ![]() x+
x+ ![]() 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.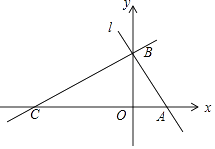
(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,解答下列问题: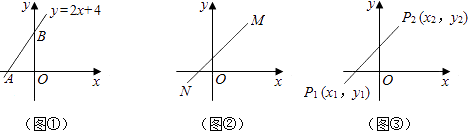
(1)如图①,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长;
(2)如图②,类比(1)的求解过程,请你通过构造直角三角形的方法,求出两点M(3,4),N(﹣2,﹣1)之间的距离;
(3)如图③,P1(x1 , y1),P2(x2 , y2)是平面直角坐标系内的两点,请你利用图③构造直角三角形,并直接写出P1P2的长度(用含有x1 , x2 , y1 , y2的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com