
【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.
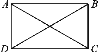
已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

【答案】(1)AC=BD,矩形;(2)证明详见解析.
【解析】
(1)根据对角线相等的平行四边形是矩形,可得答案;
(2)根据全等三角形的判定与性质,可得∠ADC与∠BCD的关系,根据平行四边形的邻角互补,可得∠ADC的度数,根据矩形的判定,可得答案.
(1)解:在平行四边形ABCD中,AC=BD,求证:平行四边形ABCD是 矩形;
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=BC.
在△ADC和△BCD中,∵AC=BD,AD=BC,CD=DC,
∴△ADC≌△BCD.∴∠ADC=∠BCD.
又∵AD∥CB,
∴∠ADC+∠BCD=180°.
∴∠ADC=∠BCD=90°.
∴平行四边形ABCD是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;②西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(![]() ):
):
(1)若该客户按方案①购买,需付款______________元(用含x的代数式表示);若该客户按方案②购买,需付款________________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
体温 | 升0.2 | 降1.0 | 降0.8 | 降1.0 | 降0.6 | 升0.4 | 降0.2 | 降0.2 | 降0 |
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)
查看答案和解析>>
科目:初中数学 来源: 题型:
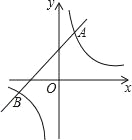
【题目】如图,一次函数y1=kx+b(k≠0)与反比例函数y2=![]() (m≠0)相交于A和B两点.且A点坐标为(1,3),B点的横坐标为﹣3.
(m≠0)相交于A和B两点.且A点坐标为(1,3),B点的横坐标为﹣3.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1≤y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
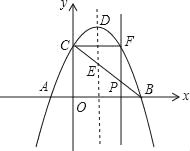
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与B,C两点重合),过点P作x轴的垂线交抛物线于点F,设点P的横坐标为m(0<m<3)
(1)当m为何值时,四边形PEDF为平行四边形;
(2)设△BCF的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.

(2)如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:将连续的偶数2,4,6,8,…,排成如表:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)移动十字框,设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2560吗?若能,写出这五个数,若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
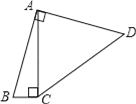
A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定x的一元一次方程ax=b的解为b﹣a,则称该方程是“差解方程”,例如:3x=4.5的解为4.5﹣3=1.5,则该方程3x=4.5就是“差解方程”,请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程4x=m是“差解方程”,则m=______.
(2)已知关于x的一元一次方程4x=ab+a是“差解方程”,它的解为a,则a+b=_____.
(3)已知关于x的一元一次方程4x=mn+m和﹣2x=mn+n都是“差解方程”,求代数式﹣3(m+11)+4n+2[(mn+m)2﹣m]﹣![]() [(mn+n)2﹣2n]的值.
[(mn+n)2﹣2n]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com