
【题目】如图,反比例函数y=![]() (n为常数,n≠0)的图象与一次函数y=kx+8(k为常数,k≠0)的图象在第三象限内相交于点D(﹣
(n为常数,n≠0)的图象与一次函数y=kx+8(k为常数,k≠0)的图象在第三象限内相交于点D(﹣![]() ,m),一次函数y=kx+8与x轴、y轴分别相交于A、B两点.已知cos∠ABO=
,m),一次函数y=kx+8与x轴、y轴分别相交于A、B两点.已知cos∠ABO=![]() .
.
(1)求反比例函数的解析式;
(2)点P是x轴上的动点,当△APC的面积是△BDO的面积的2倍时,求点P的坐标.

【答案】(1)y=![]() x+8,y=
x+8,y=![]() (2)(﹣18,0)或(6,0)
(2)(﹣18,0)或(6,0)
【解析】
(1)求得A(﹣6,0),即可得出一次函数解析式为y=![]() x+8,进而得到D(
x+8,进而得到D(![]() ,﹣2),即可得到反比例函数的解析式为y=
,﹣2),即可得到反比例函数的解析式为y=![]() ;
;
(2)解方程组求得C(![]() ,10),依据△APC的面积是△BDO的面积的2倍,即可得到AP=12,进而得到P(﹣18,0)或(6,0).
,10),依据△APC的面积是△BDO的面积的2倍,即可得到AP=12,进而得到P(﹣18,0)或(6,0).
解:(1)∵一次函数y=kx+8与y轴交于点B,
∴B(0,8).
∵在Rt△AOB中,cos∠ABO=![]() ,
,
∴tan∠BAO=![]() ,
,
∴AO=6,
∴A(﹣6,0).
∵点A在一次函数y=kx+8图象上,
∴k=![]() ,
,
∴一次函数解析式为y=![]() x+8.
x+8.
∵点D(![]() ,m)在一次函数y=kx+8图象上,
,m)在一次函数y=kx+8图象上,
∴m=﹣2,
即D(![]() ,﹣2),
,﹣2),
∵点D(![]() ,﹣2)在反比例函数y=
,﹣2)在反比例函数y=![]() 图象上,
图象上,
∴n=15.
∴反比例函数的解析式为y=![]() ;
;
(2)∵点C是反比例函数y=![]() 图象与一次函数y=
图象与一次函数y=![]() x+8图象的交点,
x+8图象的交点,
∴ ,解得
,解得 ,
,
∴C(![]() ,10).
,10).
∵△APC的面积是△BDO的面积的2倍,
∴![]() AP×10=
AP×10=![]() ×8×
×8×![]() ,
,
∴AP=12,
又∵A(﹣6,0),点P是x轴上的动点,
∴P(﹣18,0)或(6,0).


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】小明在做多项式乘法的时候发现,两个多项式相乘在合并同类项后的结果存在缺项的可能。比如x+2和x- 2相乘的结果为![]() , x的一次项没有了。
, x的一次项没有了。
(1)请计算![]() 与x-2相乘后的结果,并观察x的几次项没有了?
与x-2相乘后的结果,并观察x的几次项没有了?
(2)请想一下,![]() 与x+a相乘后的结果可不可能让一次项消失,如果可能,那么a应该是多少呢?
与x+a相乘后的结果可不可能让一次项消失,如果可能,那么a应该是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是
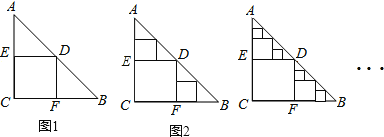
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生业余生活,决定组建绘画、摄影、读书和舞蹈兴趣活动小组,为了解学生最喜欢哪一种活动的人数,随机抽取了部分学生进行调查(每位学生必选且只能选一项),并将调查结果绘制成了两幅不完整的统计图,请你根据统计图上提供的信息回答下列问题:
(1)这次被调查的学生共有多少人,并将条形统计图补充完整;
(2)在扇形统计图中,求出最喜欢“读书”所对应的圆心角度数;
(3)若该校共有学生2000人,请你估计该校最喜欢读书活动的人数.
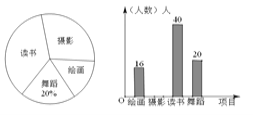
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
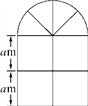
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△BCF中,点D是边CF上的一点,过点D作AD∥BC,过点B作BA∥CD交AD于点A,点G是BC的中点,点E是线段AD上一点,且∠CDG=∠ABE=∠EBF.
(1)若∠F=60°,∠C=45°,BC=2![]() ,请求出AB的长;
,请求出AB的长;
(2)求证:CD=BF+DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对连续的偶数2,4,6,8,…排成如图的形式.若将图中的十字框上下左右移动,框住的五个数之和能等于2020吗?若能,请写出这五个数中位置在最中间的数;若不能,请说明理由.你的答案是:____________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
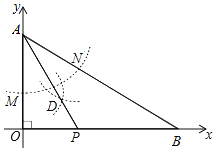
A. (1,0)B. (![]() ,0)C. (
,0)C. (![]()
![]() ,0)D. (2
,0)D. (2![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com