练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知一次函数y=kx+2，且当x=1时，y=5．
    （1）求一次函数的解析式；
    （2）将该函数图象向下平移3个单位，求平移后与x轴的交点坐标．

    分析 （1）直接把当x=1时，y=5代入一次函数y=kx+2求出k的值即可；
    （2）先求出该函数图象向下平移3个单位后的直线解析式，再令y=0，求出x的值即可．

    解答 解：（1）∵一次函数y=kx+2中，当x=1时，y=5，
    ∴5=k+2，解得k=3，
    ∴一次函数的解析式为：y=3x+2；

    （2）∵一次函数y=3x+2向下平移三个单位的解析式为y=3x-1，
    ∴当y=0时，x=$\frac{1}{3}$，
    ∴平移后与x轴的交点坐标为（$\frac{1}{3}$，0）．

    点评 本题考查的是一次函数的图象与几何变换，熟知函数图象平移的性质是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，在斜坡CM上有一棵大树AB（与水平线垂直），坡面CM与水平线CN的夹角为37°，在斜坡底端C点处测得大树顶端A的仰角为53°，已知BC间的距离为10米，求大树的高（最终结果保留整数）．（参考数据：sin37°≈$\frac{3}{5}$，tan37°≈$\frac{3}{4}$，sin53°≈$\frac{4}{5}$，tan53°≈$\frac{4}{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．关于x的一元二次方程mx2+4x+1=0有两个实数根，那么m的取值范围是m≤4且m≠0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．关于x，y的二元一次方程组$\left\{\begin{array}{l}{x+y=2k}\\{2-4y=4k+1}\end{array}\right.$的解满足x＞y，求k的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．设O是等边三角形的中心，则向量$\overrightarrow{AB}$的长度是$\overrightarrow{OA}$长度的$\sqrt{3}$倍．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知抛物线y=ax2-2ax+m与x轴相交于A（-1，0）、B两点，与y轴负半轴相交于点C，且S△ABC=6，则（　　）
    A．在y轴右侧该抛物线上不存在点M，使S△ACM=3
    B．在y轴右侧该抛物线上存在两个点M，使S△ACM=3
    C．在y轴右侧该抛物线上存在唯一的点M（2，3），使S△ACM=3
    D．在y轴右侧该抛物线上存在唯一的点M（2，-3），使S△ACM=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图1，已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使顶点B落在对角线AC边上的P处，若折痕与BC边交于点O，连接OP，AO．
    （1）求证：△POC∽△DCA；
    （2）若△POC与△ADC的面积比为1：4，求边DC的长；
    （3）如图2，在（2）的条件下，擦去折痕AO、PO，连结BP．过点A作AE⊥PB，以B为旋转中心旋转△AEB，记△A′E′B，在旋转过程中直线A′E′交AE于点F，交AC于点G，若以B，E，E′，F为顶点的四边形是正方形，求AG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

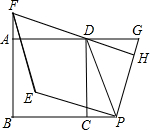    9．如图已知，四边形ABCD是正方形，点P与点G分别在线段BC与线段AD的延长线上，PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连接EF．
    求证：四边形PEFD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在?ABCD中，AB=4，AD=6，AE、DF分别平分∠BAD、∠ADC，交BC于E、F两点．
    （1）探索AE与DF的位置关系；
    （2）试求EF的长．

    查看答案和解析>>

    同步练习册答案