
【题目】一个边长为60米的正六边形跑道,P、Q两人同时从A处开始沿相反方向都跑一圈后停止,P以4米/秒逆时针方向、Q以5米/秒顺时针方向,PQ的距离为d米,设跑步时间为x秒,令d2=y,
(1)跑道全长为 米,经过 秒两人第一次相遇.
(2)当P在BC上,Q在EF上时,求y关于x的函数解析式;并求相遇前当x为多少时,他们之间的距离最大.
(3)直接写出P、Q在整个运动过程中距离最大时的x的值及最大的距离.

【答案】(1)360,40;(2)当x=24时,d的最大值为12![]() 米;(3)PQ的最大值为120米.
米;(3)PQ的最大值为120米.
【解析】
(1)由正六边形的性质可得跑道全长;根据相遇时P、Q两人的路程之和等于跑道全长列出方程,即可求解;
(2)如图,连接BF,过点Q作QH⊥BC于H,可证四边形FBHQ是矩形,可得QH=BF,而FB易求,则QH可得,显然PH就是Q跑x秒的路程减去P跑x秒的路程,于是PH可得,再由勾股定理即可求出y关于x的函数解析式,然后根据二次函数的性质求解即可;
(3)根据正六边形的性质可知:点A,B,C,D,E,F在以AD中点为圆心,AB长为半径的圆上,则可得当PQ为直径时,PQ的值最大,据此解答即可.
解:(1)∵六边形ABCDEF是正六边形,∴AB=BC=CD=DE=EF=AF=60米,
∴跑道全长=6×60=360米,
∴4x+5x=360,∴x=40s,即经过 40秒两人第一次相遇.
故答案为:360,40;
(2)∵六边形ABCDEF是正六边形,∴∠A=∠F=∠B=120°,
如图,连接BF,过点Q作QH⊥BC于H,
∵∠A=120°,AB=AF=60米,∴∠AFB=∠ABF=30°,BF=60![]() 米,
米,
∴∠BFE=∠FBC=90°,∴四边形FBHQ是矩形,
∴QH=BF=60![]() 米,FQ=BH,
米,FQ=BH,
∵AF+FQ=5x米,AB+BP=4x米,∴PH=x米,
∴y=QP2=PH2+QH2,
∴y=x2+10800,(15≤x≤24)
∴当x=24时,d的最大值为12![]() 米;
米;

(3)∵六边形ABCDEF是正六边形,∴点A,B,C,D,E,F在以AD中点为圆心,AB长为半径的圆上,
∵当x=60s时,5×60=300米,则点Q与点B重合,4×60=240米,则点P与点E重合,
∴BE为直径时,如图,P、Q之间的距离最大,
∵六边形ABCDEF是正六边形,∴BE=2AB=120米,即PQ的最大值为120米.



科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(1﹣m)x2﹣mx﹣1与x轴交于A、B两点,顶点为P.
(1)求m的取值范围;
(2)若A、B位于原点两侧,求m的取值范围;
(3)若顶点P在第四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=![]() ,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
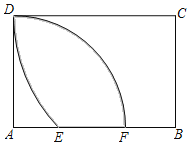
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),B(0,![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.

(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数![]() (
(![]() )的解析式;
)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com