
 2,4) 和点B (1,0)都在抛物线
2,4) 和点B (1,0)都在抛物线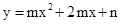 上.
上.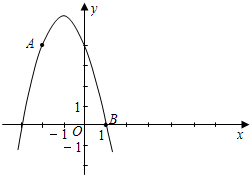
 ,4;(2)
,4;(2)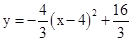 ;(3)D(3,0)或(
;(3)D(3,0)或(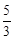 ,0).
,0). 2,4)和点B (1,0),则有:
2,4)和点B (1,0),则有: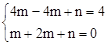 ,解得
,解得 .
.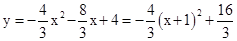 ,
, 2,4)、B (1,0),根据勾股定理可得
2,4)、B (1,0),根据勾股定理可得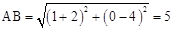 ,
,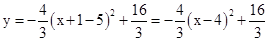 .
. 2,4),B′(6,0),∴直线AB′:
2,4),B′(6,0),∴直线AB′: .
.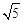 ,B′C=
,B′C=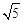 ,BC=
,BC= .
.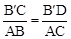 ,即
,即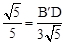 ,∴B′D=3,此时D(3,0);②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
,∴B′D=3,此时D(3,0);②∠B′DC=∠ABC,则△B′DC∽△ABC,可得: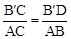 即
即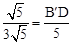 ,∴
,∴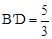 ,此时D(
,此时D(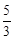 ,0).
,0).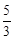 ,0).
,0).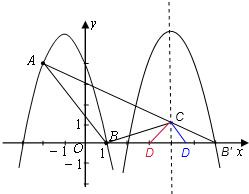


科目:初中数学 来源:不详 题型:单选题

| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,0)为圆心,以
,0)为圆心,以 为半径圆与x轴相交于点B,C,与y轴相交于点D,E.
为半径圆与x轴相交于点B,C,与y轴相交于点D,E.
 经过点C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
经过点C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
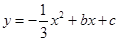 经过点A(6,0)、B(0,-4).
经过点A(6,0)、B(0,-4).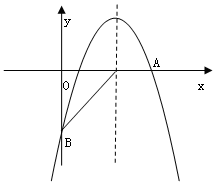
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 、F
、F 在抛物线
在抛物线 的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
 的数量关系式为:S=
的数量关系式为:S= 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com