
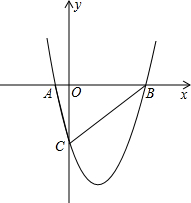
 ��ͼ����ƽ��ֱ������ϵϵxOy�У���������y=ax2+bx+c��a��0����x�ύ��A��B���㣬��y�ύ��C�㣬��ơ�ABCΪ�����ߵġ����������Ρ���
��ͼ����ƽ��ֱ������ϵϵxOy�У���������y=ax2+bx+c��a��0����x�ύ��A��B���㣬��y�ύ��C�㣬��ơ�ABCΪ�����ߵġ����������Ρ������� ��1��ֻҪ��������������Ρ���ABC�Ķ������꼴�ɽ�����⣮
��2��ֻҪ��������x�����������㣬�Ҳ�����ԭ�㼴�ɣ�
��3�������A��B�������ô���ϵ�������ɽ�����⣮
�ڷ�������������a����BC=BAʱ��A��-2��0����8��0����b����A��C=A��Bʱ����A�����߶�AB�Ĵ�ֱƽ�����ϣ��ֱ���⼴�ɣ�
��� �⣺��1����������y=x2-1��x�ύ��A��-1��0����B��1��0������y�ύ�ڣ�0��1����
�ࡰ���������Ρ���ABC�����=$\frac{1}{2}$��2��1=1��
��2��������y=ax2+bx+c��a��0�����ڡ����������Ρ���������b2-4ac��0��c��0��
��3������ͼ1�У�
�������ߵġ����������Ρ�����y��Ϊ�Գ���ĵ��������Σ�
�������ߵĶԳ���x=0��b=0��A��-3��0����B��3��0����
��0=9a+4��
��a=-$\frac{4}{9}$
�������ߵĽ���ʽΪy=-$\frac{4}{9}$x2+4��
����ͼ2�У�
��B��3��0����C��0��4����
��OA=4��OB=3��
��Rt��AOB��AB=$\sqrt{{3}^{2}+{4}^{2}}$=5��
a����BC=BAʱ��A��-2��0����8��0������ʱS��ABC=$\frac{1}{2}$��5��4=10��
b����A��C=A��Bʱ����A�����߶�AB�Ĵ�ֱƽ�����ϣ�
��ֱ��ABD ����ʽΪy=-$\frac{4}{3}$x+4��
���߶�AB���д��ߵĽ���ʽΪy=$\frac{3}{4}$x+$\frac{7}{8}$��
��A�壨-$\frac{7}{6}$��0����
��S��A��BC=$\frac{1}{2}$��$\frac{25}{6}$��4=$\frac{25}{3}$��
�����������������ߵġ����������Ρ��Dz���y��Գ���ĵ��������Σ������������Ρ������Ϊ10��$\frac{25}{3}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á����ɶ���������ϵ���������������ε��ж������ʵ�֪ʶ������Ĺؼ����������⣬ѧ���÷������۵�˼��˼�����⣬��������Ҫȫ�棬����©�⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��5��2�� | B�� | ��5��3�� | C�� | ��6��2�� | D�� | ��6��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��¼ | ��ƽ��� | ��ƽ�ұ� | ��ƽ״̬ |
| ��¼һ | 2ö1ԪӲ�Һ�7ö5��Ӳ�� | 4��10������ | ƽ�� |
| ��¼�� | 15ö1ԪӲ�� | 20ö5��Ӳ�Һ�1��10������ | ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
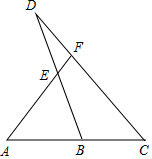 ��ͼ��BΪAC���е㣬EΪBD���е㣬��AF��AEΪ��������
��ͼ��BΪAC���е㣬EΪBD���е㣬��AF��AEΪ��������| A�� | 4��3 | B�� | 3��4 | C�� | 1��2 | D�� | 2��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽��������������̶� | |
| B�� | �˽���ϵ���̨�����Ǹ��֡���ȫ���������� | |
| C�� | �˽ⳤ�����������ֲ� | |
| D�� | �˽����•7��ѧ��ij�����IJ���ijɼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
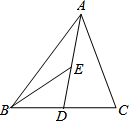 ��ͼ��BD=CD��AE=DE����ABC�������4�����ABE������ǣ�������
��ͼ��BD=CD��AE=DE����ABC�������4�����ABE������ǣ�������| A�� | 2 | B�� | 0.5 | C�� | 1 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com