
分析 根据二次根式的性质,即可解答;
(1)根据所给的例子,解析解答即可;
(2)根据所给的例子,解析解答即可.
解答 解:$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}(a≥0,b>0)$,
(1)$\sqrt{\frac{3}{100}}=\frac{\sqrt{3}}{\sqrt{100}}=\frac{\sqrt{3}}{10}$,
(2)$\sqrt{\frac{75}{27}}=\frac{\sqrt{75}}{\sqrt{27}}=\frac{5\sqrt{3}}{3\sqrt{3}}=\frac{5}{3}$,
故答案为:b,$\frac{\sqrt{3}}{10}$,$\frac{5}{3}$.
点评 本题二次根式的性质,解决本题的关键是熟记二次根式的性质.


科目:初中数学 来源: 题型:解答题
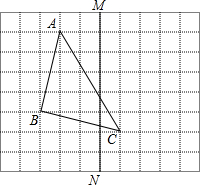 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
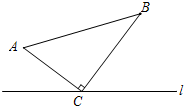 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com