
分析 (1)根据方程的系数结合根的判别式,可得出△=(m-3)2≥0恒成立,由此即可证出此方程总有实根;
(2)利用分解因式法解一元二次方程,再根据方程的两根均为正整数且m为整数,即可得出m-1=1或m-1=2,解之即可得出整数m的值.
解答 (1)证明:在方程(m-1)x2-(m+1)x+2=0中,△=[-(m+1)]2-4×2(m-1)=m2-6m+9=(m-3)2,
∵(m-3)2≥0恒成立,
∴方程(m-1)x2-(m+1)x+2=0总有实根;…(2分)
(2)解:(m-1)x2-(m+1)x+2=(x-1)[(m-1)x-2]=0,
解得:x1=1,x2=$\frac{2}{m-1}$.
∵方程(m-1)x2-(m+1)x+2=0的两根均为正整数,且m是整数,
∴m-1=1或m-1=2,
∴m=2或m=3.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)牢记“当△≥0时,方程有实数根”;(2)利用分解因式法解方程,求出x1=1,x2=$\frac{2}{m-1}$.


科目:初中数学 来源: 题型:解答题
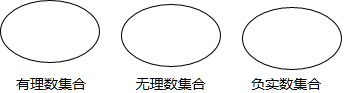 把下列各数分别填在相应的集合中:
把下列各数分别填在相应的集合中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
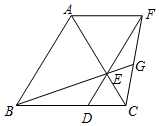 如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.
如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )
湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )| A. |  | B. |  | C. |  | D. | 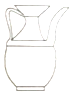 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com