
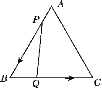
【题目】如图,△ABC是边长为3 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1 cm/s,当点P运动到B时,P,Q两点停止运动,设P点运动时间为t(s).
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y关于t的函数表达式,当t取何值时,四边形APQC的面积最小?并求出最小面积.
【答案】(1)当t为1或2时,△PBQ是直角三角形;(2)当t为![]() 时,四边形APQC的面积最小,最小面积为
时,四边形APQC的面积最小,最小面积为![]() cm2.
cm2.
【解析】
(1)分情况进行讨论:①∠BPQ=90°;②∠BQP=90°;在直角三角形中利用30°角所对直角边等于斜边一半求解即可;
(2)用△ABC的面积-△PBQ的面积表示出四边形APQC的面积,即可得出y,t的函数关系式,再将函数关系式转化为顶点式,即可求出最小值.
(1)由题意可知,∠B=60°,BP=(3-t)cm,BQ=tcm.若△PBQ是直角三角形,则∠BPQ=30°或∠BQP=30°,于是BQ=![]() BP或BP=
BP或BP=![]() BQ,即t=
BQ,即t=![]() (3-t)或3-t=
(3-t)或3-t=![]() t.解得t=1或t=2,即当t为1或2时,△PBQ是直角三角形.
t.解得t=1或t=2,即当t为1或2时,△PBQ是直角三角形.
(2)如图,过点P作PM⊥BC于点M,
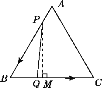
则易知BM=![]() BP=
BP=![]() (3-t)cm.
(3-t)cm.
∴PM=![]() =
=![]() (3-t)cm.
(3-t)cm.
∴S四边形APQC=S△ABC-S△PBQ=![]() ×3×
×3×![]() -
-![]() t·
t·![]() (3-t)=
(3-t)=![]() t2-
t2-![]() t+
t+![]() ,即y=
,即y=![]() t2-
t2-![]() t+
t+![]() ,易知0<t<3.
,易知0<t<3.
于是y=![]() (t-
(t-![]() )2+
)2+![]()
∴当t=![]() 时,y取得最小值,为
时,y取得最小值,为![]()
即当t为![]() 时,四边形APQC的面积最小,最小面积为
时,四边形APQC的面积最小,最小面积为![]() cm2.
cm2.


科目:初中数学 来源: 题型:
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全
班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
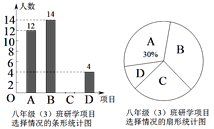
(1)八年级(3)班学生总人数是多少,并将条形统计图补充完整;
(2)宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;
(3)若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
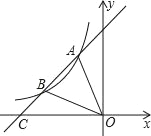
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .
查看答案和解析>>
科目:初中数学 来源: 题型:
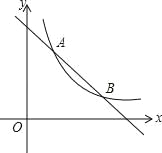
【题目】如图,一次函数 y=﹣x+4 的图象与反比例 y=![]() (k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(1)求点 A、B 的坐标及反比例函数的表达式;
(2)在 x 轴上找一点,使 PA+PB 的值最小,求满足条件的点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
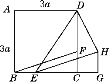
【题目】如图所示,正方形ABCD的边长为3a,两动点E,F分别从顶点B,C同时开始以相同速度沿边BC,CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B,E,C,G在一条直线上.
(1)若BE=a,求DH的长.
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
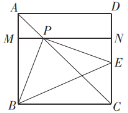
【题目】如图,P是边长为1的正方形ABCD的对角线AC上一动点(不与A、C两点重合),连接BP,过点P作PE⊥PB交直线CD于点E,连接BE,MN//BC分别交AB、DC于点M、N.设![]() .
.
(1)当点E在CD边上时,线段PE于线段PB有怎样的数量关系?试证明你的结论.
(2)设以点B,C,P,E为顶点的四边形的面积为y,试确定y与x之间的函数关系式,并求出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b(k1≠0)与双曲线![]() (k2≠0)相交于A(1,2)、B(m,﹣1)两点.
(k2≠0)相交于A(1,2)、B(m,﹣1)两点.
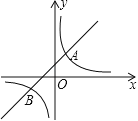
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<0<x2<x3,请直接写出y1,y2,y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com