
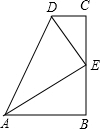
 在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 取AD的中点F,连接EF.根据平行线的性质可证得(1)(4)(5),根据梯形中位线定理可证得(3)正确.根据全等三角形全等的判定可证得(2)的正误,即可得解.
解答 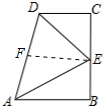 解:如图:取AD的中点F,连接EF.
解:如图:取AD的中点F,连接EF.
∵∠B=∠C=90°,
∴AB∥CD;[结论(5)]
∵E是BC的中点,F是AD的中点,
∴EF∥AB∥CD,2EF=AB+CD(梯形中位线定理)①;
∴∠CDE=∠DEF(两直线平等,内错角相等),
∵DE平分∠ADC,
∴∠CDE=∠FDE=∠DEF,
∴DF=EF;
∵F是AD的中点,∴DF=AF,
∴AF=DF=EF②,
由①得AF+DF=AB+CD,即AD=AB+CD;[结论(3)]
由②得∠FAE=∠FEA,
由AB∥EF可得∠EAB=∠FEA,
∴∠FAE=∠EAB,即EA平分∠DAB;[结论(1)]
由结论(1)和DE平分∠ADC,且DC∥AB,可得∠EDA+∠DAE=90°,则∠DEA=90°,即AE⊥DE;[结论(4)].
由以上结论及三角形全等的判定方法,无法证明△EBA≌△DCE.
正确的结论有4个.
故选C.
点评 本题考查了平行线的判定及性质、梯形中位线定理、等腰三角形的性质、全等三角形的判定等知识点,是一道难度较大的综合题型.


科目:初中数学 来源: 题型:解答题
 某地有两所中学和两条相交叉的公路(点M,N表示中学,AO,BO表示公路).计划修建一个饭馆:希望饭馆到两所中学的距离相等,到两条公路的距离也相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)
某地有两所中学和两条相交叉的公路(点M,N表示中学,AO,BO表示公路).计划修建一个饭馆:希望饭馆到两所中学的距离相等,到两条公路的距离也相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}=\frac{c}{d}$ | B. | $\frac{a}{b}=\frac{d}{c}$ | C. | $\frac{a}{c}=\frac{b}{d}$ | D. | $\frac{a}{d}=\frac{c}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com