
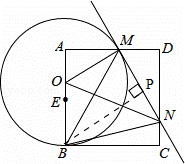
如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )
A.S1>S2+S3 B. △AOM∽△DMN C. ∠MBN=45° D. MN=AM+CN
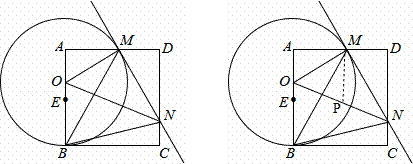 |
A解:(1)如图,作MP∥AO交ON于点P,
∵点O是线段AE上的一个动点,当AM=MD时,S梯形ONDA=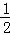 (OA+DN)•AD
(OA+DN)•AD
S△MNO=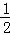 MP•AD,∵
MP•AD,∵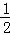 (OA+DN)=MP,∴S△MNO=
(OA+DN)=MP,∴S△MNO=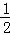 S梯形ONDA,∴S1=S2+S3,
S梯形ONDA,∴S1=S2+S3,
∴不一定有S1>S2+S3,
(2)∵MN是⊙O的切线,∴OM⊥MN,
又∵四边形ABCD为正方形,∴∠A=∠D=90°,∠AMO+∠DMN=90°,∠AMO+∠AOM=90°,∴∠AOM=∠DMN,
在△AMO和△DMN中,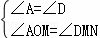 ,∴△AMO∽△DMN.故B成立,
,∴△AMO∽△DMN.故B成立,
(3)如图,作BP⊥MN于点P,
∵MN,BC是⊙O的切线,∴∠PMB=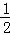 ∠MOB,∠CBM=
∠MOB,∠CBM=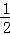 ∠MOB,
∠MOB,
∵AD∥BC,∴∠CBM=∠AMB,∴∠AMB=∠PMB,
在Rt△MAB和Rt△MPB中,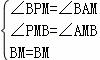 ∴Rt△MAB≌Rt△MPB(AAS)
∴Rt△MAB≌Rt△MPB(AAS)
∴AM=MP,∠ABM=∠MBP,BP=AB=BC,
在Rt△BPN和Rt△BCN中,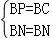 ∴Rt△BPN≌Rt△BCN(HL)
∴Rt△BPN≌Rt△BCN(HL)
∴PN=CN,∠PBN=∠CBN,∴∠MBN=∠MBP+∠PBN,
MN=MN+PN=AM+CN.故C,D成立,综上所述,A不一定成立,故选:A.


科目:初中数学 来源: 题型:
在某中学举行的演讲比赛中,初一年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差( )
| 选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 平均成绩 |
| 得分 | 90 | 95 | █ | 89 | 88 | 91 |
|
| A. | 2 | B. | 6.8 | C. | 34 | D. | 93 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=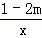 (m为常数)的图象在一、三象限.
(m为常数)的图象在一、三象限.
(1)求m的取值范围;
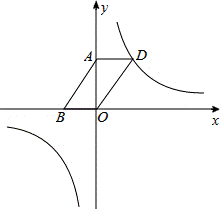
(2)如图,若该反比例函数的图象经过▱ABOD的顶点D,点A、B的坐标分别为(0,3),(﹣2,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为 ;若以D、O、P为顶点的三角形是等腰三角形,则满足条件的点P的个数为 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
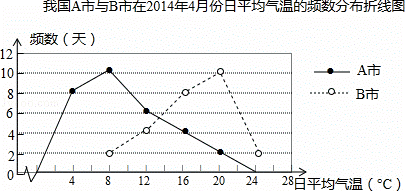
下面的频数分布折线图分别表示我国A市与B市在2014年4月份的日平均气温的情况,记该月A市和B市日平均气温是8℃的天数分别为a天和b天,则a+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知2014年3月份在某医院出生的20名新生婴儿的体重如下(单位:kg)
4.7 2.9 3.2 3.5 3.8 3.4 2.8 3.3 4.0 4.5
3.6 4.8 4.3 3.6 3.4 3.5 3.6 3.5 3.7 3.7
某医院2014年3月份20名新生儿体重的频数分布表
| 某医院2014年3月份20名新生儿体重的频数分布表 | ||
| 组别(kg) | 划记 | 频数 |
| 2.75﹣3.15 | 略 | 2 |
| 3.15﹣3.55 | 略 | 7 |
| 3.55﹣3.95 | 正一 | 6 |
| 3.95﹣4.35 | 略 | 2 |
| 4.35﹣4.75 | 略 | 2 |
| 4.75﹣5.15 | 略 | 1 |
| 合计 | 20 |
(1)求这组数据的极差;
(2)若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量(温馨提示:请在答题卷的对应位置填写,填写在试题卷上无效)
(3)经检测,这20名婴儿的血型的扇形统计图如图所示(不完整),求 :
:
 ①这20名婴儿中是A型血的人数;
①这20名婴儿中是A型血的人数;
②表示O型血的扇形的圆心角度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com