
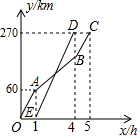
 小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.分析 (1)根据速度=路程÷时间求出小明家的最初速度,结合点C的坐标即可得出点B的坐标,再根据点B、C的坐标,利用待定系数法即可求出线段AB对应的函数解析式;
(2)根据点D、E的坐标,利用待定系数法即可求出线段DE对应的函数解析式,联立线段AB、DE对应的函数解析式成方程组,通过解方程组即可求出李叔叔追上小明家时离开家的距离,进而即可求出此时距离景区的距离.
解答 解:(1)小明家的最初的速度为60÷1=60(km/h),
点B的纵坐标为270-60×(5-4)=210.
设线段AB对应的函数解析式为y=kx+b,
将A(1,60)、B(4,210)代入y=kx+b中,
$\left\{\begin{array}{l}{k+b=60}\\{4k+b=210}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=50}\\{b=10}\end{array}\right.$,
∴线段AB对应的函数解析式为y=50x+10(1≤x≤4).
(2)设线段DE对应的函数解析式为y=mx+n,
将E(1,0)、D(4,270)代入y=mx+n中,
$\left\{\begin{array}{l}{m+n=0}\\{4m+n=270}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=90}\\{n=-90}\end{array}\right.$,
∴线段DE对应的函数解析式为y=90x-90(1≤x≤4).
联立线段AB、DE对应的函数解析式成方程组,
$\left\{\begin{array}{l}{y=50x+10}\\{y=90x-90}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2.5}\\{y=135}\end{array}\right.$,
270-135=135(km).
答:当李叔叔追上小明家时,距离景区135km.
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,解题的关键是:(1)根据点的坐标,利用待定系数法求出线段AB对应的函数解析式;(2)根据点的坐标,利用待定系数法求出线段DE对应的函数解析式.


科目:初中数学 来源: 题型:解答题
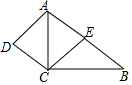 如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.
如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
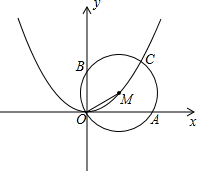 如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.
如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 不论a为何值,函数图象必经过(2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 4 | 5 | 6 | 7 |
| y | 550 | 500 | 450 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
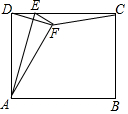 如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
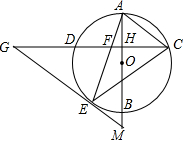 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
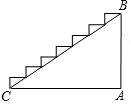 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )| A. | 3.5sin29°米 | B. | 3.5cos29°米 | C. | 3.5tan29°米 | D. | $\frac{3.5}{cos29°}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com