
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
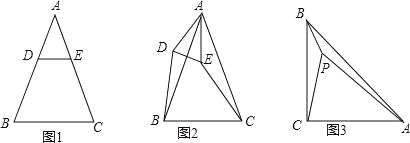
【答案】(1)=;(2)成立,证明见解析;(3)135°.
【解析】
试题分析:(1)∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∵AB=AC,∴∠B=∠C.∴∠ADE=∠AED,∴AD=EA,∴BD=CE;(2)根据旋转可得△DAB≌△EAC,从而DB=CE;(3)将△CPB绕点C旋转90°得△CEA,连接PE,可得PE=![]() ,根据PE2+AE2=AP2,推出△PEA是直角三角形.进而可求得∠BPC的度数.
,根据PE2+AE2=AP2,推出△PEA是直角三角形.进而可求得∠BPC的度数.
试题解析:(1)=;(2)成立,原因如下:由旋转可得AD=AE,∠DAB=∠CAE,又∵AB=AC,∴△DAB≌△EAC,∴DB=CE.(3)将△CPB绕点C旋转90°得△CEA,连接PE,∴△CPB≌△CEA,∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,在Rt△PCE中,![]() ,在△PEA中,PE2=(
,在△PEA中,PE2=(![]() )2=8,AE2=12=1,PA2=32=9,∵PE2+AE2=AP2,∴△PEA是直角三角形.∴∠PEA=90°,∴∠CEA=135°,又∵△CPB≌△CEA,
)2=8,AE2=12=1,PA2=32=9,∵PE2+AE2=AP2,∴△PEA是直角三角形.∴∠PEA=90°,∴∠CEA=135°,又∵△CPB≌△CEA,
∴∠BPC=∠CEA=135°.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图①,△ABC中,点D、E在边BC上,AE平分∠BAC,AD⊥BC,∠C=40°,∠B=60°,求:①∠CAE的度数;②∠DAE的度数.
(2)如图②,若把(1)中的条件“AD⊥BC”变成“F为AE延长线上一点,且FD⊥BC”,其他条件不变,求出∠DFE的度数.
(3)在△ABC中,AE平分∠BAC,若F为EA延长线上一点,FD⊥BC,且∠C=α,∠B=β(β>α),试猜想∠DFE的度数(用α,β表示),请自己作出对应图形并说明理由. 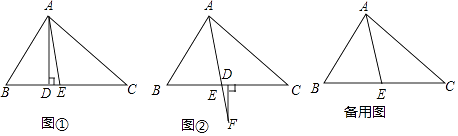
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y=-5x的图象经过第________象限,经过点(0,________)与点(1,________),y随x的增大而________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com