
| �����ط� ���� ���� | ���� | ���� | ||||||
| ���� | 70 | 60 | 50 | 40 | 50 | 60 | 70 | 80 |
| ���� | 30 | 40 | 50 | 60 | 30 | 20 | 10 | 0 |

| �����ط� ���� ���� | ���� | ���� | ||||||
| ���� | 70 | 60 | 50 | 40 | 50 | 60 | 70 | 80 |
| ���� | 30 | 40 | 50 | 60 | 30 | 20 | 10 | 0 |
| x���֣� | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| y����Ԫ�� | 17.8 | 17.7 | 17.6 | 17.5 | 17.4 | 17.3 | 17.2 |




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �У�ֱ��
�У�ֱ�� ����
����| A����һ�����������ޣ� | B����һ�����������ޣ� |
| C����һ�����������ޣ� | D���ڶ������������ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �Ľ���______________��
�Ľ���______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

 .ij������ÿ�춼Ҫ���������
.ij������ÿ�춼Ҫ���������
 ����Ʒһ������A������B��.�ܸ����������ƣ�����ֻ�ܲ�ȡ�������ͻ��е�һ�ֽ�������������ǰԤ��.���л����շ���Ŀ���շѱ�������ʻ·
����Ʒһ������A������B��.�ܸ����������ƣ�����ֻ�ܲ�ȡ�������ͻ��е�һ�ֽ�������������ǰԤ��.���л����շ���Ŀ���շѱ�������ʻ· /
/
 ����ʻʱ��
����ʻʱ�� /s�ĺ���ͼ����ͼ1�������ܻ���������ͳ��ͼ����ͼ2������Ϣ���£�
/s�ĺ���ͼ����ͼ1�������ܻ���������ͳ��ͼ����ͼ2������Ϣ���£�| ���乤�� | ����ѵ���Ԫ/�� �� ��  �� �� | ��طѵ���Ԫ/�� ��h�� ��h�� | �̶�����Ԫ/�� |
| ���� | 2 | 5 | 200 |
| �� | 1.6 | 5 | 2280 |

 /h�����ٶ�Ϊ
/h�����ٶ�Ϊ 
 /h��
/h��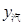 /Ԫ��
/Ԫ��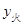 /Ԫ���ֱ���
/Ԫ���ֱ���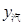 ��
��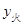 ��
�� �ĺ�����ϵʽ������д��
�ĺ�����ϵʽ������д�� ��ȡֵ��Χ������
��ȡֵ��Χ������ Ϊ��ֵʱ
Ϊ��ֵʱ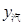 ��
��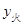 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com