
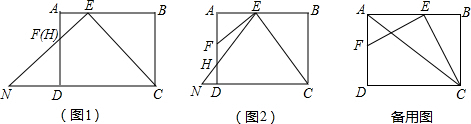
分析 (1)求出∠BEC=45°,推出BE=BC,即可得出答案;
(2)过点E作EG⊥CN,垂足为点G,推出BE=CG,求出∠N=∠ECN,得出EN=EC,推出CN=2CG=2BE,又知CD=AB=4即可得出答案;
(3)求出∠AFE=∠CEB,推出∠HFE=∠AEC,分为两种情况:(ⅰ)若∠FHE=∠EAC时,推出∠EAC=∠ECB,求出tan∠EAC=tan∠ECB,代入$\frac{BC}{AB}$=$\frac{BE}{BC}$求出BE即可;(ⅱ)若∠FHE=∠ECA,EG与AC交于点O.求出∠AHE=∠BCE,∠ENC=∠ECN.求出∠CEG=∠ECA,推出EO=CO,设EO=CO=3k,则AE=4k,AO=5k,根据AO+CO=8k=5求出k,求出AE=$\frac{5}{2}$,BE=$\frac{3}{2}$,即可得出答案
解答 解:(1)如图1,∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠AEF=∠BEC,
∴∠BEC=45°,
∵∠B=90°,
∴BE=BC,
∵BC=3,
∴BE=3; (2)如图2,过点E作EG⊥CN,垂足为点G,
(2)如图2,过点E作EG⊥CN,垂足为点G,
∴BE=CG,
∵AB∥CN,
∴∠AEH=∠N,∠BEC=∠ECN,
∵∠AEH=∠BEC,
∴∠N=∠ECN,
∴EN=EC,
∴CN=2CG=2BE,
∵CD=AB=4,
∴2BE-DN=4;
(3)如图3,∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠AFE+∠AEF=90°,
∵EF⊥EC,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴∠HFE=∠AEC,
当以点E,F,H为顶点的三角形与△AEC相似时,
(ⅰ)若∠FHE=∠EAC时,
∵∠BAD=∠B,∠AEH=∠BEC,
∴∠FHE=∠ECB,
∴∠EAC=∠ECB,
∴tan∠EAC=tan∠ECB,
∴$\frac{BC}{AB}$=$\frac{BE}{BC}$,
∴BE=$\frac{9}{4}$,
∴DN=$\frac{1}{2}$;
(ⅱ)若∠FHE=∠ECA,如图3,EG与AC交于点O.
∵∠AEH=∠BEC,
∴∠AHE=∠BCE,∠ENC=∠ECN.
∵EN=EC,EG⊥CN,
∴∠HEG=∠CEG,
∵AH∥EG,
∴∠FHE=∠HEG,
∴∠FHE=∠CEG,
∴∠CEG=∠ECA,
∴EO=CO,
设EO=CO=3k,则AE=4k,AO=5k,
∴AO+CO=8k=5,
∴k=$\frac{5}{8}$,
∴AE=$\frac{5}{2}$,BE=$\frac{3}{2}$,
∴DN=1,
综上所述,线段DN的长为$\frac{1}{2}$或1
点评 本题考查了平行线性质,矩形性质,相似三角形的性质和判定,直角三角形斜边上中线性质,等腰三角形的性质和判定的应用,主要考查学生综合运用定理进行推理和计算的能力,题目比较好,但是难度偏大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,小虎站在自己家的A处,测得某信号塔CD的顶点C的俯角∠EAC为37°,底部D点的俯角∠EAD为50°,已知小虎家距地面的高度AB为60m.
如图,小虎站在自己家的A处,测得某信号塔CD的顶点C的俯角∠EAC为37°,底部D点的俯角∠EAD为50°,已知小虎家距地面的高度AB为60m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
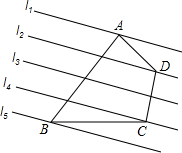 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
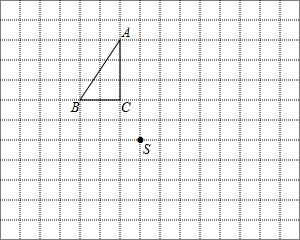 △ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.
△ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (-$\sqrt{3}$)2=9 | C. | $\root{3}{-9}$=-3 | D. | ±$\sqrt{9}$=±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的极差是8 | |
| D. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次一定有4次中奖 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com