
分析 (1)将t=3代入解析式可得;
(2)根据h=10可得关于t的一元二次方程,解方程即可;
(3)由题意可得方程20t-t2=m 的两个不相等的实数根,由根的判别式即可得m的范围.
解答 解:(1)当t=3时,h=20t-5t2=20×3-5×9=15(米),
∴当t=3时,足球距离地面的高度为15米;
(2)∵h=10,
∴20t-5t2=10,即t2-4t+2=0,
解得:t=2+$\sqrt{2}$或t=2-$\sqrt{2}$,
故经过2+$\sqrt{2}$或2-$\sqrt{2}$时,足球距离地面的高度为10米;
(3)∵m≥0,由题意得t1,t2是方程20t-5t2=m 的两个不相等的实数根,
∴b2-4ac=202-20m>0,
∴m<20,
故m的取值范围是0≤m<20.
点评 本题主要考查二次函数背景下的求值及一元二次方程的应用、根的判别式,根据题意得到相应的方程及将实际问题转化为方程问题是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
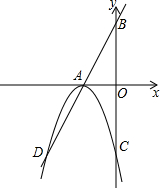 如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,
如图,直线AB解析式为y=2x+4,C(0,-4),AB交x轴于A,A为抛物线顶点,交y轴于C,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
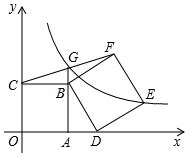 如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.
如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | AB=AD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 2016年里约热内卢奥运会(即第31届夏季奥林匹克运动会)开幕式将于当地时间8月5日在马拉卡纳体育场举行.如图是第31届夏季奥林匹克运动会会徽图案,下列关于它的对称性判定正确的是( )
2016年里约热内卢奥运会(即第31届夏季奥林匹克运动会)开幕式将于当地时间8月5日在马拉卡纳体育场举行.如图是第31届夏季奥林匹克运动会会徽图案,下列关于它的对称性判定正确的是( )| A. | 只是轴对称图形 | |
| B. | 只是中心对称图形 | |
| C. | 既不是轴对称图形也不是中心对称图形 | |
| D. | 既是轴对称图形也是中心对称图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com