
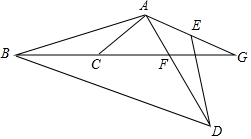
 如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.
如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )| A. | 23° | B. | 22° | C. | 32° | D. | 33° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.
如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,高BF、CE相交于点H.
如图,在△ABC中,高BF、CE相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.
如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com