
(11·珠海)(本题满分9分)如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,
AD=AB=1,BC=2.将点A折叠到CD边上,记折叠后A点对应的点为P(P与D点不重
合),折痕EF只与边AD、BC相交,交点分别为E、F.过点P作PN∥BC交AB于N、交
EF于M,连结PA、PE、AM,EF与PA相交于O.
(1)指出四边形PEAM的形状(不需证明);
(2)记∠EPM=a,△AOM、△AMN的面积分别为S1、S2.


(1)四边形AMPE为菱形 ……………………2分
(2)证明:∵四边形AMPE为平行四边形, EPM=a
∴∠MAP=a S1=OA·OM. ……………………4分
∵在Rt△OM中,tan=,∴OM=OA·tan.
==OA·OM×=OA2=×(PA)2=PA2.……………………5分
(3)过D作DH垂直于BC于H,交NP于点K,

则:DK⊥PN,BH=AB=AD=DH=1,DK=AN=x.
∵CH=BC-BH=2-1=1,
∴CH=DH.
∴∠NPD=∠BCD=45°.
∴PK=DK=x.
∴PN=1+x.
在Rt△ANP中,
AP2=AN 2+PN 2=x2+(1+x)2=2x2+2x+1. ……………………6分
过E作PM的垂线EG(垂足为G),令△EGM的面积为S.
∵△EGM∽△AOM,
∴=()2==.
则S= S1.
∵四边形ANGE的面积等于菱形AMPE的面积,
∴2S1=S2+S.
∴S1-S2=S-S1= S1-S1=(-1)S1.
∴y==(-1)×
=(-1)× PA2= (4x2-AP2).
∴y=x2-x-.
解析:略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
(11·珠海)(本题满分9分)已知:如图,锐角△ABC内接于⊙O,∠ABC=45°;
点D是![]() 上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
BE,AD的垂线AF与DC的延长线交于点F.
(1)求证:△ABD∽△ADE;
(2)记△DAF、△BAE的面积分别为S△DAF、S△BAE,求证:S△DAF>S△BAE.

查看答案和解析>>
科目:初中数学 来源: 题型:
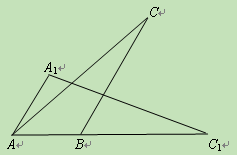
(11·珠海)(本题满分7分)如图,将一个钝角△ABC(其中∠ABC=120°)绕
点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
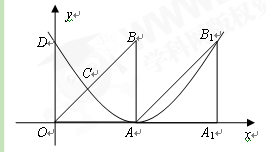
(11·珠海)(本题满分7分)如图,Rt△OAB中,∠OAB=90°,O为坐标原点,
边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后
得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·珠海)(本题满分7分)某校为庆祝国庆节举办游园活动,小军来到摸球
兑奖活动场地,李老师对小军说:“这里有A、B两个盒子,里面都装有一些乒乓球,你只
能选择在其中一只盒子中摸球.”获将规则如下:在A盒中有白色乒乓球4个,红色乒乓球
2个,一人只能摸一次且一次摸出一个球,若为红球则可获得玩具熊一个,否则不得奖;在
B盒中有白色乒乓球2个,红色乒乓球2个,一人只能摸一次且一次摸出两个球,若两球均
为红球则可获得玩具熊一个,否则不得奖.请问小军在哪只盒子内摸球获得玩具熊的机会更
大?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com