
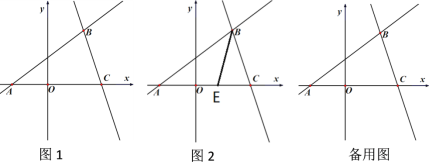
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴交于点A,且经过点B(2,m),点C(3,0).
轴交于点A,且经过点B(2,m),点C(3,0).
(1)求直线BC的函数解析式;
(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;
(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M的坐标;
(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒![]() 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4) t最小值为
;(4) t最小值为![]() 秒
秒
【解析】
(1)把B(2,m)代入直线l解析式可求出m的值,即可得B点坐标,设直线BC的解析式为y=kx+b,把B、C两点坐标代入可求得k、m的值,即可的直线BC的解析式;(2)过点O作![]() 交BC于点D,可知S△ABC=S△ABD,
交BC于点D,可知S△ABC=S△ABD,![]() ,联立直线BC与OD的解析式解得交点D的坐标即可;(3)分别讨论P点在y轴的负半轴和正半轴时两种情况,①P点在y轴的负半轴时,作
,联立直线BC与OD的解析式解得交点D的坐标即可;(3)分别讨论P点在y轴的负半轴和正半轴时两种情况,①P点在y轴的负半轴时,作![]() 于点N,可证明△AOP
于点N,可证明△AOP![]() △PNM1,设
△PNM1,设
OP=NM1=m,ON=m-2,则M1的坐标为(m,2-m),代入BC解析式即可求出m的值,进而可得M1坐标;②当P点在y轴正半轴时,同①解法可求出M2的坐标,综上即可得答案;(4)作射线AQ与x轴正半轴的夹角为45°,过点B作x轴的垂线交射线AQ于点Q,作![]() 于点K,作
于点K,作![]() 于点T,可求出AG、AQ、BQ的长,根据时间t=
于点T,可求出AG、AQ、BQ的长,根据时间t=![]() +
+![]() =BE+EK≥BT,利用面积法求出BT的值即可.
=BE+EK≥BT,利用面积法求出BT的值即可.
(1)解:将点B(2,m)代入![]() 得m=3
得m=3
∴![]()
设直线BC解析式为![]() 得到
得到![]()
∴![]()
∴直线BC解析式为![]()
( 2 )如图,过点O作![]() 交BC于点D
交BC于点D
∴S△ABC=S△ABD,![]()
∴直线OD的解析式为y=![]() x,
x,
∴
解得

![]()
(3)①如图,当P点在y轴负半轴时,作![]() 于点N,
于点N,
∵直线AB与x轴相交于点A,
∴点A坐标为(-2,0),
∵∠APO+∠PAO=90°,∠APO+∠PNM1=90°
∴∠PAO=∠PNM1,
又∵AP=PM1,∠POA=∠PNM1=90°
∴△AOP![]() △PNM1,
△PNM1,
∴PN=OA=2,
设OP=NM1=m,ON=m-2
∴![]()
解得![]()
![]() ∴
∴![]()

②如图,作![]() 于点H
于点H
可证明△AOP![]() △PHM2
△PHM2
设HM2=n,OH=n-2
∴![]()
解得![]()
∴M2(![]() ,
,![]() )
)

∴综上所述![]() 或M2(
或M2(![]() ,
,![]() ).
).
(4)如图,作射线AQ与x轴正半轴的夹角为45°,过点B作x轴的垂线交射线AQ于点Q,作![]() 于点K,作
于点K,作![]() 于点T,
于点T,
∵∠CAQ=45°BG⊥x轴,B(2,3)
∴AG=4,
∴AQ=4![]() ,BQ=7,
,BQ=7,
t=![]() =BE+EK≥BT,
=BE+EK≥BT,
由面积法可得:![]()
∴![]() ×4
×4![]() ×BT=
×BT=![]() ×7×4,
×7×4,
∴BT=![]()
因此t最小值为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量![]() (件)与时间
(件)与时间![]() (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间![]() 之间的函数关系式.(2分)
之间的函数关系式.(2分)
(2)求乙组加工零件总量![]() 的值.(3分)
的值.(3分)
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?(5分)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC经过平移后得到△DEF,点A与点D,点B与点E,点C与点F分别是对应点,已知点A(3,3)、D(-2,1),解答下列问题:
(1)请在坐标系中画出平移后的△DEF;
(2)请直接写出以下点的坐标:B(___,___)、C(___,___)、E(___,___)、F(___,___);
(3)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),则P点坐标为(____,____).

查看答案和解析>>
科目:初中数学 来源: 题型:
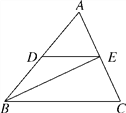
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com