����⣺��1����Rt��ABC�У�OB=1��OA=3����CO��AB��
��OC=
=
���� C��0��-
����
�������ߵĽ���ʽΪ��y=a��x+1����x-3���������C������ã�
a��0+1����0-3��=-
��a=
�������ߵĽ���ʽ��y=
��x+1����x-3��=
x
2-
x-
��
��2����֪OA=3��OB=1��OC=
����S
��ABC=
AB•OC=
��4��
=2
��
�ٵ���P��x���Ϸ�ʱ��������֪��S
��ABP=
S
��ABC����
��P��x��ľ�����ڵ�C��x������һ�룬�� ��P��������Ϊ
��
��y=
x
2-
x-
=
������ã�2x
2-4x-9=0
��� x=
��
��P
1��
��
����P
2��
��
����
�ڵ���P�������ߵ�B��C��ʱ����Ȼ��BCP�����ҪС��
S
��ABC����������������⣻
�۵���P�������ߵ�A��C��ʱ��S
��ACP=
AC•h=
S
��ABC=
����h=1��
������CK��ȡ��D��ʹ��CD=h=1������D��ֱ��DE��l
1����y���ڵ�E������ͼ��
��Rt��CDE�У���ECD=��BCO=30�㣬CD=1����CE=
��OE=OC+CE=
����E��0��-
��
��ֱ��DE��y=
x--
�����������ߵĽ���ʽ���У�
����ã�
��
��P
3��1��-
����P
4��2��-
����
���ϣ����ڷ��������ĵ�P��������Ϊ��
��
������
��
������1��-
������2��-
����

��3���ɣ�1��֪��y=
x
2-
x-
=
��x-1��
2-
��
�������ߵĶԳ��� x=1��
��Rt��OBC��OB=1��OC=
�����BCO=��1=30�㡢��2=��3=90��-��BCO=60�㡢BC=2��
����C��ֱ��CN��x�ᣬ���������ڵ�N������ͼ��
�������ߵĶԳ��Կɵã�N��2��-
�������� CN=2��
��ֱ֪��BC��y=-
x-
���� K��1��-2
����CK=
=2��
�ڡ�CKN�У���2=60�㣬CN=CK=2����ô��CKN�ǵȱ�������----�٣�
��KC=KMʱ����C��M���������ߵĶԳ���Գƣ����Ϣٵ����������M��N�غϣ�
��KC=CNʱ������KC=BC�����Դ�ʱ��M��B��N�غϣ�
��MK=MCʱ����M���߶�CK���д����ϣ�CK���д������������ཻ�ڵ�N�����ཻ�������ߵĶ��㣮
���ϣ�����������ֱ��l
1����ת�ǶȦ�=60����=��ACN=90��-��2=30�㣮

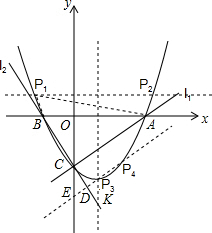
 ��2012•�ɻ���һģ����֪��ֱ��l1��l2�ֱ���A��3��0������B��-1��0�������ҵ�����ֱ��ͬʱ�ཻ��y�Ḻ����ĵ�Cʱ��ǡ����l1��l2��������A��B��C�������ߵĶԳ�����ֱ��l2���ڵ�K����ͼ��ʾ��
��2012•�ɻ���һģ����֪��ֱ��l1��l2�ֱ���A��3��0������B��-1��0�������ҵ�����ֱ��ͬʱ�ཻ��y�Ḻ����ĵ�Cʱ��ǡ����l1��l2��������A��B��C�������ߵĶԳ�����ֱ��l2���ڵ�K����ͼ��ʾ�� ��2����֪OA=3��OB=1��OC=
��2����֪OA=3��OB=1��OC= ��3���ɣ�1��֪��y=
��3���ɣ�1��֪��y=


 ��2012•�ɻ���һģ����ͼ��Rt��ABC�У���C=90�㣬BC=3cm��AB=5cm����P�ӵ�A������AC��1.5cm/s���ٶ����C�����˶��������C��������ԭ�����ٶ���CA���أ���Q�ӵ�B������BA��1cm/s���ٶ����A�����˶���������P��Q���˶���DE���ִ�ֱƽ��PQ���ҽ�PQ�ڵ�D��������PC-CB-BQ�ڵ�E����P��Qͬʱ����������Q�����Aʱֹͣ�˶�����PҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0������t=
��2012•�ɻ���һģ����ͼ��Rt��ABC�У���C=90�㣬BC=3cm��AB=5cm����P�ӵ�A������AC��1.5cm/s���ٶ����C�����˶��������C��������ԭ�����ٶ���CA���أ���Q�ӵ�B������BA��1cm/s���ٶ����A�����˶���������P��Q���˶���DE���ִ�ֱƽ��PQ���ҽ�PQ�ڵ�D��������PC-CB-BQ�ڵ�E����P��Qͬʱ����������Q�����Aʱֹͣ�˶�����PҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0������t= ��2012•�ɻ���һģ��ij������һ������εĿյ���ͼ��ʾ��Ϊ�������������ּƻ�������θ�����ΪԲ�ģ�2m��Ϊ�뾶������������Ӱ���֣����ϻ��ݣ���ô���ϻ��ݵ����������������
��2012•�ɻ���һģ��ij������һ������εĿյ���ͼ��ʾ��Ϊ�������������ּƻ�������θ�����ΪԲ�ģ�2m��Ϊ�뾶������������Ӱ���֣����ϻ��ݣ���ô���ϻ��ݵ����������������