
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数,例如M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min(3,1,1)=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min(3,1,1)=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= .②min{2![]() ,3
,3![]() ,4}= .
,4}= .
(2)若min(3﹣2x,1+3x,﹣5)=﹣5,则x的取值范围为 .
(3)若M{﹣2x,x2,3}=2,求x的值.
(4)如果M{2,1+x,2x}=min{2,1+x,2x},求x的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=kx+1(k≠0)与直线x=k,直线y=﹣k分别交于点A、B,直线x=k与直线y=﹣k交于点C,
(1)求直线l与y轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段AB、BC、CA围成的区域(不含边界)为W.
①当k=1时,区域内的整点有 个,其坐标为 .
②当k=2时,区域W内的整点有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校今年学生节期间准备销售一种成本为每瓶4元的饮料.据去年学生节试销情况分析,按每瓶5元销售,一天能售出500瓶;在此基础上,销售单价每涨0.1元,该日销售量就减少10瓶.针对这种饮料的销售情况,请解答以下问题:
(1)设销售单价为每瓶x元,当日销售量为y元,求y与x的函数关系式(不写出x的取值范围);
(2)设该日销售利润为w元,求w与x的函数关系式(不写出x的取值范围);
(3)该日销售利润为800元,求销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
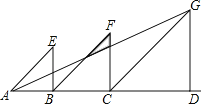
【题目】三个等腰直角三角形Rt△ABE,Rt△BCF,Rt△CDG如图摆放在射线AD上,直角顶点分别为B,C,D,已知相似比为2:3:4,AB=4,则(1)CG的长为_____;(2)图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
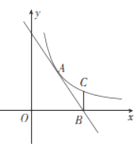
【题目】如图,反比例函数y=![]() (x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
(x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
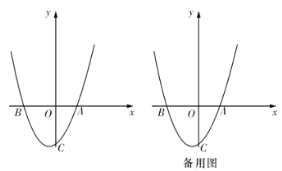
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于
轴相交于![]() 点,对称轴为
点,对称轴为![]() ,直线
,直线![]() 与抛物线相交于
与抛物线相交于![]() 、
、![]() 两点.
两点.
(1)求此抛物线的解析式;
(2)![]() 为抛物线上一动点,且位于
为抛物线上一动点,且位于![]() 的下方,求出
的下方,求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=![]() (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.

(1)求反比例函数和一次函数的解析式.
(2)连接OB,MC,求四边形MBOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com