
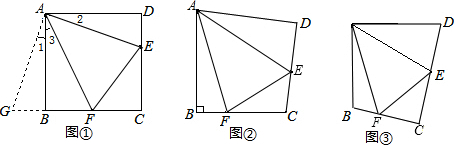
 ��ͼ���ڡ�ABC�У�BA=BC=20cm��AC=30cm����P��A��������AB��4cm/s���ٶ����B�˶���ͬʱ��Q��C���������CA��3cm/s���ٶ���A���˶������˶�ʱ��Ϊx��s����
��ͼ���ڡ�ABC�У�BA=BC=20cm��AC=30cm����P��A��������AB��4cm/s���ٶ����B�˶���ͬʱ��Q��C���������CA��3cm/s���ٶ���A���˶������˶�ʱ��Ϊx��s�������� ��1����PQ��BCʱ������ƽ���߷��߶γɱ����������ɵó�����AP��PQ��AB��AC�ı�����ϵʽ�����ǿɸ���P��Q���ٶȣ���ʱ��x��ʾ��AP��AQ��Ȼ����ݵó��Ĺ�ϵʽ���x��ֵ��
��2������Ҫ����������������ۣ���֪�ˡ�A�͡�C��Ӧ��ȣ���ô��Ҫ�ֳ�AP��CQ��Ӧ�ɱ����Լ�AP��BC��Ӧ�ɱ��������������x��ֵ��
��3�����ݵȸ�����ȵ��ڵıȣ����ɵõ����ۣ�
��� �⣺��1��������ã�PQƽ����BC����AP��AB=AQ��AC��AP=4x��AQ=30-3x
��$\frac{4x}{20}$=$\frac{30-3x}{30}$
��x=$\frac{10}{3}$��
��2�������������ο������ƣ�
���1������APQ�ס�CQBʱ��CQ��AP=BC��AQ��
����$\frac{3x}{4x}$=$\frac{20}{30-3x}$���x=$\frac{10}{9}$��
�����飬x=$\frac{10}{9}$��ԭ��ʽ���̵Ľ⣮
��ʱAP=$\frac{40}{9}$cm��
���2������APQ�ס�CBQʱ��CQ��AQ=BC��AP��
����$\frac{3x}{30-3x}$=$\frac{20}{4x}$���x=5��
�����飬x=5��ԭ��ʽ���̵Ľ⣮
��ʱAP=20cm��
����������AP=$\frac{40}{9}$cm��AP=20cm��
�ʴ�Ϊ��$\frac{40}{9}$cm��20cm��
��3����S��BCQ��S��ABC=1��3ʱ��$\frac{CQ}{AC}$=$\frac{1}{3}$��
��$\frac{AQ}{CQ}=\frac{2}{1}$��
��CQ��AC=1��3��AC=30����CQ=10=3x��x=$\frac{10}{3}$����AP=4x=$\frac{40}{3}$��
��AP��AB=$\frac{40}{3}$��20=2��3��
���� ������Ҫ���������������ε��ж������ʣ��������������Ƶó��߶αȻ�������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
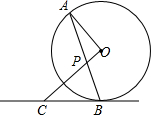 ��ͼ��AB�ǡ�O���ң�OP��OA��AB�ڵ�P������B�ġ�O�����߽�OP���ӳ����ڵ�C��
��ͼ��AB�ǡ�O���ң�OP��OA��AB�ڵ�P������B�ġ�O�����߽�OP���ӳ����ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | һ�� | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
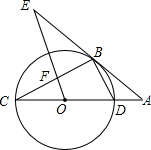 ��ͼ��ʾ��CDΪ��O��ֱ������B�ڡ�O�ϣ�����BC��BD������B������AE��CD���ӳ��߽��ڵ�A��OE��BD����BC�ڵ�F����AB�ڵ�E��
��ͼ��ʾ��CDΪ��O��ֱ������B�ڡ�O�ϣ�����BC��BD������B������AE��CD���ӳ��߽��ڵ�A��OE��BD����BC�ڵ�F����AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��-1�� | B�� | ��-1��1�� | C�� | ��-1��-3�� | D�� | ��-1��3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com